半径aの2つの円O.O´が2点A.Bで交わっている。中心間の距離O.O´が√3a（√3✖️a）の時共

半径aの2つの円O.O´が2点A.Bで交わっている。中心間の距離O.O´が√3a（√3✖️a）の時共通部分の面積と四角形AOBO´の面積の比を教えてください。

No.1 回答者： majimelon37 回答日時： 2018/11/28 17:44

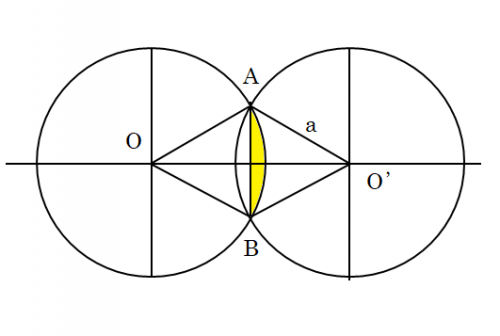
半径aの2つの円O.O' が2点A.Bで交わっている。

中心間の距離O.O´が√3a（√3✖️a）の時共通部分の面積と四角形AOBO'の面積の比を教えてください。

半径aの2つの円O.O'が2点A.Bで交わっていて、中心間の距離O.O'が√3aのときは、三角形OABと三角形O'ABは一辺がaの正三角形である。一つの正三角形の面積は、(√3/4)a²だから、四角形AOBO'の面積は、正三角形２つ分で、(√3/2)a²である。
次に円弧AOBは、∠AOBが60°だから、円の1/6でその面積は(1/6)πa²である。これから正三角形AOBを切り取ると、黄色く色を付けた三日月形が残る。
黄色い三日月形の面積は(1/6)πa²－(√3/4)a²である。
2つの円の共通部分は、黄色い三日月形２個だから、面積は(1/3)πa²－(√3/2)a²
共通部分の面積と四角形AOBO'の面積の比は
((1/3)πa²－(√3/2)a²)/(√3/2)a²=2π/3√3－1≒0.2092