物理 点電荷
真空中に直行するxy座標軸を取り、原点Oからそれぞれ距離a[m]の点A(−a、0)と点B(a、0)
にそれぞれ電気量Q[C]の正の点電荷を固定する。クーロンの法則の比例定数をKとし、無限遠点での電位を0とする。
(1)点AとBの電荷がつくる電場中で、y軸上の負の向きに十分離れた点に用意した電気量−Q[C]の負電荷をy軸上に沿って点D(0,−a)まで移動させ固定した。このとき必要な外力を求めよ。
(2)その後、点Aにある正の点電荷と点Dにある負の点電荷を置き換えた。この置き換えに必要な仕事は何Jか?
A 回答 (1件)
- 最新から表示
- 回答順に表示
No.1
- 回答日時:
直行するxy座標軸→直交するxy座標軸
D(0,y)のとき、AD、BDの距離rは、r=√(a^2+y^2)_①である。
(1)
クーロンの法則F=KQ1Q2/r^2、クーロンポテンシャル= KQ/rの式を使う。
AとDにある電荷の間のポテンシャルエネルギーはE=-KQ^2/r
BとDにある電荷の間のポテンシャルエネルギーもE=-KQ^2/r
二つを加えてE=-2KQ^2/r=-2KQ^2/√(a^2+y^2)
力F=-∂E/∂y=-2KQ^2(-1/2)/ (a^2+y^2)^(3/2)・2y
=KQ^2(2y)/ (a^2+y^2)^(3/2)
ここで、Dの座標y=-a を入れると
F=-KQ^2(2a)/ (a^2+a^2)^(3/2) =-KQ^2(2a)/ (2a^2)^(3/2)
=-KQ^2(2a)/ (2a^2)√((2a^2)) =-KQ^2/ (a^2√2)
Dにある電荷をこの位置に止めるには、-y方向で大きさKQ^2/ (a^2√2)の力が必要。
(2)
点Aにある正の点電荷と点Dにある負の点電荷を置き換える。
Aにある電荷とDにある電荷は符号が変わる。
置き換え前の電荷の間のエネルギーEは
(1)AとBの間のEは、E=KQ^2/2a
(2)AとDの間のEは、E=-KQ^2/(√2 a)
(3)BとDの間のEは、E=-KQ^2/(√2 a)
置き換え後の電荷の間のエネルギーEは
(4)AとBの間のEは、E=-KQ^2/2a
(5)AとDの間のEは、E=-KQ^2/(√2 a)
(6)BとDの間のEは、E=KQ^2/(√2 a)
置き換え後のEの合計から置き換え前のEの合計を引くと、
(2)と(5)は消し合う、-(1)=(4) -(3)=(6)
(4)+ (5)+ (6)-((1)+ (2)+ (3))= (4)+(6)-((1)+ (3)) = (4)+(6)+ (4)+(6) = ((4)+(6))×2
=(-KQ^2/2a+ KQ^2/(√2 a))×2= KQ^2 /a(-1/2+1/√2 ))×2
= (√2-1)KQ^2 /a
置き換えに必要な仕事は(√2-1)KQ^2 /a[J]
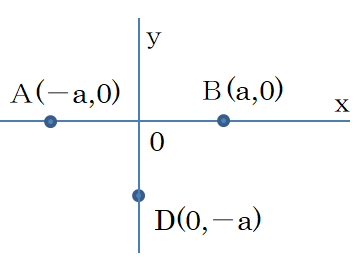
お探しのQ&Aが見つからない時は、教えて!gooで質問しましょう!
似たような質問が見つかりました
- 物理学 高校物理、点電荷がつくる電場・電位の問題です。 1 2023/06/19 20:20
- 物理学 高校物理、点電荷がつくる電場、電位の問題です。 1 2023/06/18 22:44
- 物理学 電磁気学 クーロン力についての問題です。 xy平面上の原点に電荷量 1[C]の点電荷が,点 P(2, 3 2023/08/05 23:41
- 物理学 xy平面上の点A(- 2, 0)に電荷量3[C]の点電荷が、点B(3, 0)に電荷量-2[C]の点電 2 2023/08/14 21:15
- 物理学 xy平面上の原点に電荷量 1[C]の点電荷が,点 P(2,0) に電荷量-3[C]の点電荷が置かれて 4 2023/08/13 17:03
- 物理学 大学物理 1 2023/01/28 15:15
- 物理学 xy平面上の点A(- 2, 0)に電荷量3[C]の点電荷が、点B(3, 0)に電荷量-2[C]の点電 3 2023/08/13 22:12
- 物理学 xy平面上の点A(- 2, 0)に電荷量-2[C]の点電荷が、点B(3, 0)に電荷量3 [C]の点 2 2023/08/05 23:44
- 物理学 xy平面上の原点(0,0)に電荷qの点電荷を置き、点A(a,0)に電荷量-3qの点電荷を置く。ただし 3 2023/08/11 23:01
- 物理学 電荷の受ける力 1 2023/02/04 17:51
関連するカテゴリからQ&Aを探す
おすすめ情報
デイリーランキングこのカテゴリの人気デイリーQ&Aランキング
マンスリーランキングこのカテゴリの人気マンスリーQ&Aランキング
-
ファンデルワールス力とは何ですか
-
金(Au)を人工的に作れない理...
-
電子はどこから来て、どこへ行く?
-
電気は、なぜ流れるのでしょうか?
-
塩化アンモニウムはなぜ金属元...
-
p+、p++、n-、n--の意味は?
-
化学のアボガドロ定数の公式の2...
-
構成と組成の意味の違い
-
電磁気学の2つの同心導体球の電...
-
炭酸カルシウムCaCO3のCaの酸...
-
SF作品における「プラズマ砲...
-
原子間力について
-
反発係数の最も高い物質は?
-
金属について
-
なぜ放射線は水の中を通れない...
-
wt%からat%に変換する方法
-
疎水コロイドについて
-
スピン量子数
-
半反応式の疑問
-
2つの物質の比重が同じであれ...
おすすめ情報
