No.4ベストアンサー
- 回答日時:
(1)
C:y=x^3-2x+1 ...(A)
y'=3x^2-2
点(t,t^3-2t+1)における接線
y=(3t^2-2)(x-t)+t^3-2t+1 ...(B)
(B)が点点A(2,-3)を通ることから
-3=(3t^2-2)(2-t)+t^3-2t+1
整理して
-2(t-3)t^2=0
∴ t=0, 3 …(1)の答え
なお、接線は
t=0の時 y=-2x+1
t=2の時 y=25x-53
(2)
B(2,a)を通るCの接線は (B)より
a=(3t^2-2)(2-t)+t^3-2t+1
a=-2t^3+6t^2-3 ...(C)
点B(2,a)を通るCの接線が3本存在する条件から
tの3次方程式(C)が異なる3実数を持てば良い。
すなわち
y=a ...(D)
y=g(t)=-2t^3+6t^2-3 ...(E)
とおけば(D)と(E)のグラフが異なる3交点を持てば良い。
(E)のグラフについて
g'(t)=-6t(t-2), g''(t)=-12(t-1)
g'(t)=0の時 t=0,2
t=0の時 g''(0)=12>0 , 極小値f(0)=-3
t=2の時 g''(2)=-12(<0), 極大値f(2)=5
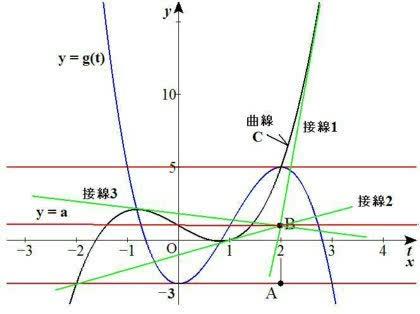
y=g(t)のグラフの概形を描くと添付図の青線のようになる。
(増減表を作って(E)のグラフの概形を描いて下さい)
点B(2,a)を通る曲線Cの接線が添付図の緑線のように3本引けるための条件は(E)のグラフにx軸に平行な直線(D)(赤線グラフ)と異なる3交点を持てば良い。すなわち
-3<a<5 …(2)の答え
No.3
- 回答日時:
y=x^3-2x+1上の点(t,t^3-2t+1)における接線は
y’=3x^2-2より
y-( t^3-2t+1)=( 3t^2-2)(x-t)
整理して
y=( 3t^2-2)x-2t^3+1
(1)これがA(2,-3)を通ることから
-3=( 3t^2-2)2-2t^3+1
整理して
t^3-3t^2=0
この解は
t=0 又は t=3
(2) これがB(2,a)を通ることから
a=( 3t^2-2)2-2t^3+1
整理して
a=-2t^3+6t^2-3
y=a
と
y=-2t^3+6t^2-3 (1)
の交点を考えればよい
(1)をtで微分して
dy/dt=-6t^2+12t=-6t(t-2)
(1)はt=0で極小(極小値は-3)、t=2で極大(極大値は13)
(増減表を書いて曲線の概要を図示すること。)
答え
-3<a<13
No.2
- 回答日時:
待てw 問一はマジで教科書レベルだぞ。
関学ってこんなサービス問題を出すのか!?ということで、教科書を見直しましょう。この問題すら分からなければ、志望校の
ランクを相当落とさないと行けない。
お探しのQ&Aが見つからない時は、教えて!gooで質問しましょう!
似たような質問が見つかりました
- 数学 接線の本数を求めたいときの与式の微分について FG例題206 f(x)=xe^-x とするとき、 実 4 2023/07/24 15:43
- 数学 微分積分の変曲点、接線についての問題がわからないです。 1 2023/01/08 13:41
- 数学 三次関数 点A(2、a)を通って、曲線y=x^3-3xに三本の接線が引けるようなaの値を求めよ 少し 2 2023/07/02 16:09
- 数学 数学 標高zがz=x^2-y^2で与えられている地形を、点Pが水準面上で曲線(x,y)=(t,t^2 3 2023/08/03 21:52
- 数学 数学の問題について 1 2023/02/13 18:40
- 数学 微分積分の曲率についての問題がわからないです。 4 2022/07/16 16:23
- 数学 【 数I 放物線と直線の共有点 】 問題 放物線y=x²+ax+bが点(1,1)を通り, 直線y=2 4 2022/07/18 09:57
- 数学 球面と接する直線の軌跡が表す領域 4 2023/07/30 12:37
- 数学 数学 2時間数に関わる問題について教えてください。 x≧1 y≧-1 2x+y=5 であるとき、xy 7 2022/10/29 10:57
- 高校 三次関数のグラフにつきまして 3 2022/05/15 11:14
おすすめ情報
デイリーランキングこのカテゴリの人気デイリーQ&Aランキング
-
曲線と点の最短距離の出し方
-
エクセル2007曲線の接線と傾き...
-
Excelでこの直線と曲線が離れ出...
-
数IIIの放物線の問題です
-
点(1,a)から曲線y=e^(-x^2)に異...
-
数字で分かりません…
-
tを正の実数とする。放物線G:y=...
-
円の接線はなぜ接点を通る半径...
-
放物線
-
包絡線がわかりません
-
接線の公式の導き方の教科書の...
-
数学の極限の問題です。 limx→0...
-
放物線と接線(数C)
-
漸近線と接線のちがいについて
-
数2 円と直線 点(1.2)を通り...
-
放物線と接線
-
「接する」の厳密な定義とは?
-
接触する二球の接点の高さ
-
サイクロイドは円を転がす…じゃ...
-
数学の問題です。
マンスリーランキングこのカテゴリの人気マンスリーQ&Aランキング
-
曲線と点の最短距離の出し方
-
常にf’’(x)>0とf’'(x)=0...
-
数2の関数の接線の問題なのです...
-
円の接線
-
傾きが同じ?
-
エクセル2007曲線の接線と傾き...
-
3次関数と、直線が変曲点で接す...
-
傾きから接線の方程式を求めるには
-
点(a,b)の存在範囲
-
Excelでこの直線と曲線が離れ出...
-
数学の問題です。
-
y=e^xに対して点(0、a)から...
-
【数学】 接点が異なれば、接線...
-
放物線
-
変曲点について。
-
微分について教えてください 放...
-
三次関数 点A(2、a)を通って、...
-
漸近線と接線のちがいについて
-
数学の問題で、わからないので...
-
微分の接線についての問題です
おすすめ情報
