関数f(x)＝x^ 3−3ax^2＋3bx−2 が区間0≦x≦1 で常に単調増加するとき、点(a.b

関数f(x)＝x^ 3−3ax^2＋3bx−2 が区間0≦x≦1 で常に単調増加するとき、点(a.b)の存在する範囲を図示せよ。
という問題で、解答に
0＜x＜1 において f'(x)≧0 となればよい。
とかいてあるのですが、
なぜf'(x)＞0 と違ってイコールがつくのかわかりません。
似たような質問をみたら広義単調増加、狭義単調増加、、とかいてあったのですがよくわからないので質問させていただきました。

No.2 ベストアンサー 回答者： むらさめ 回答日時： 2018/02/10 23:38

f(x)＝x^3-3ax^2＋3bx-2

f’(x)＝3x^2-6ax＋3b
=3(x^2-2ax＋b)

区間0≦x≦1 で常に単調増加　①
0≦x≦1　x=0,1　の時、f’(x)が増加しない、即ち接線の傾きが0になったら①の条件にそぐわなくなるからです。

No.6 回答者： majimelon37 回答日時： 2018/02/16 12:10

f(x)＝x^ 3−3ax^2＋3bx−2を微分するとf ' (x)は式(1)となる。

f ' (x)＝3x^ 2−6ax＋3b＝3(x－a)^2＋3b－3a^2＿＿式(1)
この問題では狭義の単調増加であるが、狭義か広義かの抽象的な論義では解決しない。
問題に即して考えるために、まず、問題を解く。
単調増加になるためには、f ' (x)≧０は必要であるが、単調増加になるかならぬかの限界を調べる。
　下図左にその限界状態のf ' (x)のグラフのA,B,C,Dの４通りを示した。f ' (x)は2次の項が3x^ 2であるから、どのグラフも同じ形の放物線になる(合同である)。限界状態のグラフはAとB,CとDの３通りに分けられる。Aは区間[0,1]の左端のｘ＝０にくっ付いて、これより下に下がると、f ' (x)＜０になる。
Dは区間[0,1]の右端のｘ＝1にくっ付いて、これより下に下がると、f ' (x)＜０になる。
BとDは放物線の最下端がｘ軸上の区間[0,1]に接触し、これより下に下がると、f ' (x)＜０になる。
この三つに分類した時の条件は、次の式になる。
A：f ' (0)=0、D：f ' (1)=0、BとDはf ' (a)＝０で０≦a≦1
である。許される」領域を不等式で書けば
A：f ' (0)= 3b≧0、D：f ' (1)=3－6a+3b≧0、BとDはf ' (a)＝3b－3a^2≧0で０≦a≦1
これを整理して、次の３条件をすべて満たす領域が求める範囲である。
b≧0、b≧2a－1、b≧a^2　(０≦a≦1)
下図右に示す二つの直線と、放物線の一部(０≦a≦1の部分)より上にある範囲である。
　下図左で、放物線は一点のみで区間[0,1]に接触する。この一点以外ではf ' (x)＞０であるから狭義単調増加が保証されている。残るのはｘ＝a，(０≦a≦1)の一点であるが、増加とはＰ＜Ｑの２点があって、f (Ｐ)＜f (Q)ならば増加という。一点だけでは比較することができないから、P，Qは異なる点で、たとえばf ' (Ｐ)＝０であれば、必ずf ' (Q)＞０であるから狭義単調増加である。

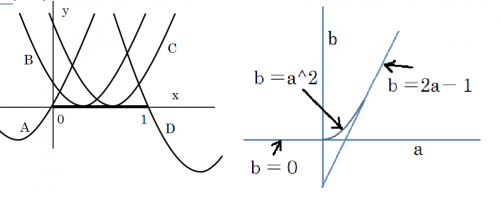
No.5 回答者： クソgooは死ね 回答日時： 2018/02/11 01:33

その問題では, 単調増加は狭義単調増加の意味で使われています.

>なぜf'(x)＞0 と違ってイコールがつくのかわかりません。
例えば, a = 1/3, b = 1/9 の場合で考えてみてください.

No.4 回答者： sc348253 回答日時： 2018/02/11 01:02

具体的に考えてみてはどうでしょうか！？ つまり、

実際問題として、3次関数としてありえませんが、
x=0 で、f'(x)=0 で、暫くの間 f'(x)=0 が続く、横に伸びる感じで、ある時から上に上がる場合が、xの増加に従って、f(x)が、減らない場合を広義的単調増加と言いますから、
可能性として、f'(x)=0も含まれますね！
単調増加の定義を調べてみてはどうでしょうか？

No.3 回答者： 3345677 回答日時： 2018/02/11 00:03

むさらめさん

傾きがマイナスにならない限り単調増加だから、f'(x)＝0も条件を満たすのでは？「傾き0」は「単調増加」であるための十分条件ではないけど必要条件である。つまり、傾きが0は単調増加であるという条件を満たす。

No.1 回答者： 3345677 回答日時： 2018/02/10 23:27

f'(x)＝0のとき、f(x)の傾きは0、つまり増加も減少もしません。

これを広い意味で捉える(広義)と、増加に入ります。傾きが0は、増加と考えるのです。