三角関数 至急!!!

三角関数って
角度の数値
以外では
値は一切決まらないものですよね???

質問者からの補足コメント

• 扇形で直線部と弦または弧の長さとかでも。
  
  これらから三角関数の値ってわかるんですか？

  No.2の回答に寄せられた補足コメントです。 補足日時：2021/03/15 18:10

• 角度の概念以外のすべての数値です。　辺の長さ等です。

  No.3の回答に寄せられた補足コメントです。 補足日時：2021/03/15 18:31

• 三角関数の場合　
  引数が　θ　ということですか?

  No.5の回答に寄せられた補足コメントです。 補足日時：2021/03/15 22:06

• 三角関数の引数は
  θ以外にも
  ありますよね?

  No.7の回答に寄せられた補足コメントです。 補足日時：2021/03/16 09:13

No.9 回答者： ありものがたり 回答日時： 2021/03/20 11:30

＞扇形で直線部と弦または弧の長さとかでも。

＞これらから三角関数の値ってわかるんですか？

中心角以外でも、中心角と一対一に対応しているものからなら
中心角に対する三角関数の値は決められます。
でも、それは弦や弧長が三角関数の引数だってこととは
話が微妙に違いますよね。ただ、弦や弧長から中心角が求まる
ってだけで。

No.8 回答者： Arima01 回答日時： 2021/03/16 21:31

> 三角関数の引数は

> θ以外にも
> ありますよね?

関数は、『関数名（引数）』の形なので。
sin(θ)であれば、θが引数。
sin(2θ)であれば、2θが引数。
sin(x+2nπ)であれば、x+2nπが引数。

質問はこう言うことですかね？

No.7 回答者： Arima01 回答日時： 2021/03/15 22:35

> 三角関数の場合　

> 引数が　θ　ということですか?

そう言うことです。
一般に『関数名（引数）』の形になります。

例：sin(θ)、f(x)、log(x)など


ちなみに、No.6が弧度法を熱弁してるのは分かるのですが。
『三角関数は弧度法で定義されている』とおっしゃっているのですが、ずっと言っている、「三角関数の定義」のソースを提示しないことには否定も肯定も致しかねます。

No.6 回答者： t_fumiaki 回答日時： 2021/03/15 21:23

引数の単位は本質的な意味があります。

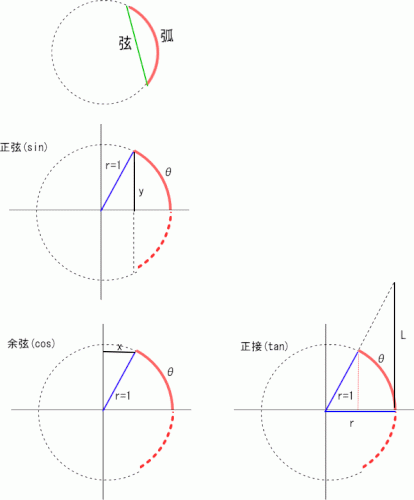
単位円の弧の長さθを三角関数に入力すると、弦の長さ、及び接線の長さが求まる、と言うのが三角関数の定義です。

一般の円(半径r)の場合には、半径rで割って、単位円に変換しています。

大元の定義(単位円)
y(弧の側の弦の長さ)=sin(弧の長さ)
x(弧と逆側の弦の長さ)=cos(弧の長さ)
l(弧の側の接線の長さ)=tan(弧の長さ)

半径rの一般の円、全部をrで割って単位円に変換する
y/r=sin(弧の長さ/r)
x/r=cos(弧の長さ/r)
l/r=tan(弧の長さ/r) [下図の右でl/r=y/xになる事が解ると思う]

必然的に弧の長さ/r、つまり弧の長さのラジアン値が要求されるのです。

角度では無く、円弧のラジアン値を角のところで使ってるだけです。

「度数法」で、定義し直すと、微分・積分が厄介になる為、「度数法」での再定義はしていないのです。

sinx°をxで微分すると、(π/180)cosx°となり、(π/180)の係数がストーカーの様に付きまとうのが、「度数法」での再定義をしていない理由です。

No.5 回答者： Arima01 回答日時： 2021/03/15 20:36

https://ja.wikipedia.org/wiki/%E4%B8%89%E8%A7%92 …

http://w3e.kanazawa-it.ac.jp/math/category/sanka …

上を見る限り、三角関数の引数において、角度の単位を「弧度法」に限定してるとは思えません。単位は「度数法」でも問題ないと思います。定義のソースが欲しいところですが。そもそも単位に本質的な意味はないはずです。

ただ、微積分などの公式や計算は弧度法を前提としているため、一般的に弧度法を用いるのが無難。

sin(), cos(), tan(), log()などの全ての"関数"は、引数によって値が一意に決まります。
なので、sinθなどで、θが確定すれば、sinθも確定します。
逆に、θが確定しなければ、sinθも確定しません。

三角形の辺が確定すれば、角度も確定するため、最終的に関数値が確定すると言うことです。

No.4 回答者： t_fumiaki 回答日時： 2021/03/15 19:51

「角度の数値」って言うのは定義違反。

その角度に対応する円弧の長さを半径で割ったラジアンが定義。

つまりsin30°と言うのは定義に無い。
正しくはsin(π/6)

三角関数の定義をキチンと確認した方が良い。
解らなければ、補足するから言う様に。

No.3 回答者： yhr2 回答日時： 2021/03/15 18:09

「角度の数値以外」って、例えばどんなもの？

No.2 回答者： mukaiyam 回答日時： 2021/03/15 18:05

直角三角形で 2 辺の長さを提示すれば sin も cos tan も求まりますけど。

同様に、扇形で直線部と弦または弧の長さとかでも。

No.1 回答者： angkor_h 回答日時： 2021/03/15 18:00

はい、その通りです。

三角関数は、角度を基にした関数です。