５４０との最大公約数が１であるものは〔アイウ〕個である

５４０との最大公約数が１であるものは〔アイウ〕個である

アイウに入る解答はなんでしょうか？
すみませんが解いてください

解き方も教えてほしいです
お願いします。

No.7 ベストアンサー 回答者： wild_kit 回答日時： 2010/10/05 06:17

　もっと簡単そうな解き方がありますね。

(^_^;)
要するに全体の数から２の倍数、３の倍数、５の倍数を除けばよいのです。
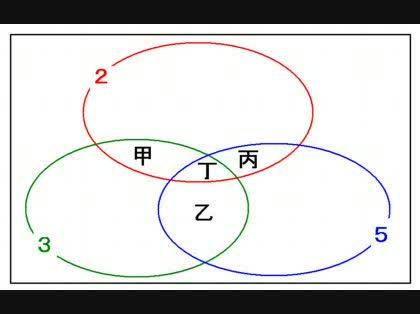
　図もご覧ください。
２の倍数の個数は５４０／２＝２７０
３の倍数の個数は５４０／３＝１８０
５の倍数の個数は５４０／５＝１０８
以上を足すと５５８
２・３の倍数として重複して数えている個数は５４０／６＝９０（甲＋丁）
３・５の倍数として重複して数えている個数は５４０／１５＝３６（乙＋丁）
２・５の倍数として重複して数えている個数は５４０／１０＝５４（丙＋丁）
２・３・５の倍数として３回数えられている個数は５４０／３０＝１８（丁）
甲＋乙＋丙＋丁ｘ２を５５８から引きたい
（甲＋丁）＋（乙＋丁）＋（丙＋丁）－丁　＝９０＋３６＋５４－１８　＝１６２
５５８－１６２＝３９６
これが２または３または５の倍数の個数です。
これを全体の数から引けば、２でも３でも５でも割り切れない数の個数となります。
５４０－３９６＝１４４
以上でよろしいでしょうか？？

この回答へのお礼

画像まで、説明ありがとうございます！
すごく分かりやすいです☆

お礼日時：2010/10/05 06:54

No.6 回答者： himajin100000 回答日時： 2010/10/05 05:54

>#3

2*2*7と540は最大公約数が1である、ということですね。

この回答へのお礼

ありがとうございます！

お礼日時：2010/10/05 06:55

No.5 回答者： wild_kit 回答日時： 2010/10/05 02:59

　少し補足します。

３桁までの数ｚの一番上の桁の数をａ、真ん中の桁の数をｂ、一番下の桁の数をｃとして表すとします。
それはｚ＝１００ａ＋１０ｂ＋ｃということであり、変形すると９９ａ＋９ｂ＋（ａ＋ｂ＋ｃ）となります。
つまりその数が３で割れるということは、ａ＋ｂ＋ｃが３の倍数ということです。
ということで（３）が出てきているわけです。

　下１桁が（１，７）・（１，３，７，９）・（３，９）の繰り返しになるのは、上２桁が３ｙ・３ｙ＋１・３ｙ＋２の繰り返しになるからです。（ｙは０以上の整数）

この回答へのお礼

ありがとうございます！

お礼日時：2010/10/05 06:55

No.4 回答者： wild_kit 回答日時： 2010/10/05 02:13

　５４０＝２＾２ｘ３＾３ｘ５

従って（１）偶数ではない　（２）下１桁が５ではない　（３）各桁の数字を足したものが３の倍数で無いものを探すことになります。
上２桁が００なら下１桁は１，７
上２桁が０１なら下１桁は１，３，７，９
上２桁が０２なら下１桁は３，９
上２桁が０３なら下１桁は１，７
以下同様に繰り返します。
　ここで上２桁に注目します。
００から０２を１ユニットと考えると５３までに何ユニットあるでしょう？？（該当する数は５４０未満の自然数ですから。）
ユニット数＝上２桁に１を加えたものを３で割った答の整数部ですね。
すると（５３＋１）／３＝１８ユニットあります。
１ユニットに付き該当する数は８個あります。
従って８ｘ１８＝１４４個あると思われます。
ア＝１、イ＝４、ウ＝４

この回答へのお礼

詳しい説明ありがとうございます！

お礼日時：2010/10/05 06:52

No.3 回答者： sanori 回答日時： 2010/10/05 01:40

そうでしたか。

５４０を素因数分解すると
５４０　＝　２^2×３^3×５

したがって、
２^a　×　３^b　×　５^c
（ａ＝０～２、　ｂ＝０～３、ｃ＝０～１、ただし、ａ＝ｂ＝ｃ＝０　だけはダメ）
は、５４０と１以外の公約数を持ちます。

　　たとえば、ａ＝１、ｂ＝２、ｃ＝０　だと、
　　２^1　×　３^2　×　５^0　＝　２×９×１　＝　１８
　　となり、１８と５４０は、１以外の公約数を持ちます。

したがって、５４０と１以外の公約数を持つ５４０以下の自然数の個数は、
（２＋１）×（３＋１）×（１＋１）　－　１　＝　２３
３４２
よって、５４０との最大公約数が１である５４０以下の自然数の個数は、
５４０　－　２３　＝　５１７
です。

No.2 回答者： windwald 回答日時： 2010/10/05 01:30

540は2で割り切れるので、2や4や8などは540との最小公倍数が1ではありません。

つまり、５４０との最大公約数が１であるものは2の倍数ではありません。
以下同様に考えます。

この回答へのお礼

ありがとうございます

お礼日時：2010/10/05 06:51

No.1 回答者： sanori 回答日時： 2010/10/04 23:57

こんにちは。

たとえば、５４０より大きい素数は、５４０との最大公約数が１になります。
しかし、そのような素数は無限個あるので、
アに「む」、イに「げ」、ウに「ん」と書くぐらいでしょうか。

問題文がおかしいと思います。

この回答への補足

すみません前半の部分を省いてました。

【問】
５４０以下の自然数のうち、２でも３でも割り切れないものは(１８０)個ある。
さらに、５４０との最大公約数が１であるものは○○○個である。



という問題なんですが、この場合も解なしでしょうか？

補足日時：2010/10/05 00:23