数学の問題が分かりません

中1の数学の問題が分かりません。
(1)，(2)どちらもです。分かる方
回答、解説お願いしますm(_ _)m

質問者からの補足コメント

• 問題文↓
  次の図は、点A，B，C，D，E，F，G，Hを頂点とする正四角柱であり、底面の1辺の長さが6㎝，高さが10㎝である。辺DH上に点P，辺BF上に点QをDP＝BQとなるようにとり、3点C，P，Qを通る平面でこの四角形を切ったら、その切り口である四角形CPRQはひし形になった。切ってできた２つの立体のうち、頂点Aをふくむ方の立体を「立体ア」、頂点Fをふくむ方の立体を「立体イ」とするとき、次の問いに答えなさい。
  
  (1)「立体イ」の体積が270㎤であるとき、BQの長さを求めなさい。
  
  (2)「立体イ」の表面積が「立体ア」の表面積より96㎠大きいとき、BQの長さを求めなさい。

  
    補足日時：2015/03/01 10:23

• (1)の問題は、「立体ア」が90㎤であるところまで
  だしました。そこから先の解説お願いします。
  
  (2)の問題は、まったく分かりません。答えが３㎝に
  なるそうです。解説お願いします。

    補足日時：2015/03/01 10:40

No.2 ベストアンサー 回答者： ORUKA1951 回答日時： 2015/03/01 14:08

多分幾何の単元ではなく、方程式の単元だと思います。

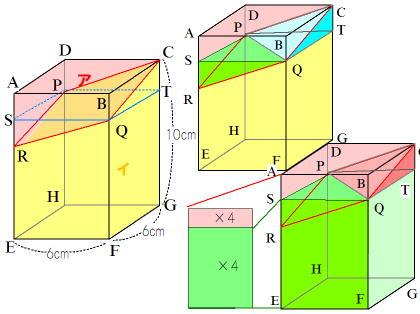
(1) PQを含む底面に平行な平面でこの直方体を切って、A-E、C-Gとの交点をS,Tとすると、三角錐(PQSR)(緑)と三角錐(PQTC)(水色)は合同ですから、アの体積は、四角柱(ABCD-高さBQ)と同じですから、その体積が90cm³によって、
　90(cm³) = 6 × 6 × h (cm³)　　hはBQの長さ
　h = 90 × 1/6 × 1/6
　　= 90/36
　　= 5/2
(2) 同様に、表面積の差は、
　96(cm²) = 6 × (10 - h) × 4 　-　 6 × h × 4
　　　　　　四角柱(EFHH-SQTP)　　四角柱(ABCD-SQTP)
　96 = 24(10 - h) - 24h
　　　= 240 - 24h - 24h
　　　= 240 - 48h
　240 - 96 = 48h
　　　144 = 48h
　　　　 3 = h

この回答へのお礼

解説ありがとうございますm(_ _)m
図があり、とても分かりやすかったです。

お礼日時：2015/03/01 18:09

No.1 回答者： ORUKA1951 回答日時： 2015/03/01 09:58

首をひねって、ピンボケで読みにくいものを読んで答えろと？？

　少なくとも問題文をテキストで打ち直すくらいの努力はしましょう。解説や回答を書く手間が簡単になります。よく読んで正確に書き写すだけで問題文や聞かれていることが理解できるはずです。それで自分で解き方が見えてくるものです。
　文章題は問題自体はとても簡単なものです。ポイントは読解力--国語--ですよ。国語力がない人は数学はできません。
※努力したけど、ここが分からないとポイントを絞って質問すると、ずれた解説しなくてすむし、そもそも努力した形跡があれば手を差し伸べたくなる物です。

この回答へのお礼

アドバイスありがとうございますm(_ _)m
問題文書きました。教えてもらう立場なので
回答者様に伝わりにくい質問は、確かに良く
なかったです。以後、気をつけます。

お礼日時：2015/03/01 10:46