数学I なんで正三角形の内心は一致するのか

タイトルのままです。
今日課題を出されました。
明日まで考えてこいっと・・・・・・。

何度考えてもなぜ正三角形の内心は一致するのかが
わかりません(´・ω・`)

教えてください!!

ちなみにあたしは高１です。
出来るだけわかりやすくしていただけると
嬉しいです(゜∀゜)

No.8 回答者： arrysthmia 回答日時： 2009/02/26 12:35

内心 ＝ 三角形の　各内角の二等分線　３本の交点

外心 ＝ 三角形の　各辺の垂直二等分線　３本の交点
重心 ＝ 三角形の　各中線(頂点と対辺の中点を結ぶ線)　３本の交点
垂心 ＝ 三角形の　各頂点から対辺へ降ろした垂線　３本の交点

各「○心」の存在は、証明済みとして…

正三角形において、
　　内角の二等分線と
　　辺の垂直二等分線と
　　中線と
　　頂点から対辺へ降ろした垂線と
が、一致することを示せば ok。

No.7 回答者： rukuku 回答日時： 2009/02/26 01:24

ゴメンナサイ

m(__)m
回答に間違いがありました。
課題には間に合わないと思いますが、訂正します。

外心の方の証明が違います。

正三角形で、重心と内心・外心が同じであることの証明は
内心と重心とが同じことの証明⇒左の図の赤線が同じ長さの証明
外心と重心とが同じことの証明⇒右の図の赤線が同じ長さの証明
です。

そのため外心の方は、前の回答の「ピンクと水色」ではなく、「ピンクとむらさき」の部分の合同を証明する必要があります。

No.6 回答者： mister_moonlight 回答日時： 2009/02/25 20:07

正三角形は、重心・内心・垂心・外心は全て一致する。

高1なら、初等幾何でいくか。書込みが面倒だから、コピーしてきた。ｗ

[重心→内心]
正三角形ABCの重心をGとする．
このとき，重心の性質からAGとBCの交点をLとするとLはBCの中点．
△ABL≡△ACLからAL，すなわちAGは∠BACを二等分する．
同様にBGは∠ABCを，CGは∠BCAを二等分するのでGは△ABGの内心。

[内心→垂心]
正三角形ABCの内心をIとする．
AIとBCとの交点をPとすれば△ABP≡△ACPで，∠APB=∠APC=90°，すなわちAI⊥BC．
同様にBI⊥CA，CI⊥ABから、Iは△ABCの垂心．

[垂心→外心]
正三角形ABCの外心をHとする．
AHとBCとの交点をVとすればAV⊥BC，AB=ACから△ABV≡△ACV．
したがってAHはBCの垂直二等分線となる．
同様にBHはCAの，CHはABの垂直二等分線となり，Hは△ABCの外心．

[外心→重心]
正三角形ABCの外心をOとする．
このときOA=OB=OC，BC=CA=ABから△OBC≡△OCA≡△OABとなり，OAとBCの交点をXとすればBX：XC=△OAB：△OAC=1:1となるから、XはBCの中点．
同様にOBとACの交点，OCとABの交点もぞれぞれAC,ABの中点になるので　Oは△ABCの重心．

以上よりすべて一致する．

この回答へのお礼

わざわざ長い解説ありがとうございます。
コピーしてきたものでも嬉しいですよ!!

助かりました。

お礼日時：2009/02/25 23:52

No.5 回答者： rukuku 回答日時： 2009/02/25 20:04

訂正です

×「重心」の定義を中学の数学を使うとできます。
○「重心」の定義と中学の数学を使うとできます。

No.4 回答者： rukuku 回答日時： 2009/02/25 20:00

続きです。

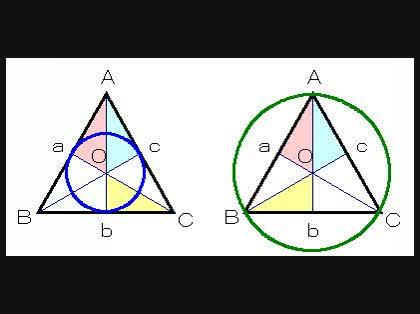
図中の点Ｏは重心とします。

このＯが内心はと一致することを証明するには、
△ＡａＯ
△ＡｃＯ
△ＣｂＯ
の３つの三角形が合同であることを証明すればＯＫです。
⇒Ｏａ=Ｏｂ=Ｏｃが証明できます。


同じように、
Ｏが外心と一致することを証明するには、
△ＡａＯ
△ＡｃＯ
△ＢｂＯ
の３つの三角形が合同であることを証明すればＯＫです。
⇒ＯＡ=ＯＢ=ＯＣが証明できます。

では、それぞれ３つの三角形が合同なのをどうやって証明するのかということは、手間はかかりますが、「重心」の定義を中学の数学を使うとできます。

この回答へのお礼

rukukuさん何度も来ていただいきありがとうございます(＾＾)

画像つきでとてもわかりやすいです。

明日までには頑張って理解をしたいと思います。
参考になりました!!

お礼日時：2009/02/25 23:44

No.3 回答者： rukuku 回答日時： 2009/02/25 19:56

はじめまして

正三角形では、重心と外心と内心はすべて一致します。
証明は三角形の合同を上手く使えばできます。
（詳細は今作成中ですので少々お待ちください）

定義はこちら
http://www.geisya.or.jp/~mwm48961/math2/sansin.htm

No.2 回答者： sanori 回答日時： 2009/02/25 19:37

こんばんは。

まず、外心は、コンパスで３頂点を通る円を描くときの、コンパスの針の部分です。
コンパスの針の位置を、点Ｏとします。

では、内心が、点Ｏとは違う位置にある点Ｐだとしましょう。
そして、コンパスの針で刺したまま１２０度回転します。
すると、回転する前とそっくりな状況になります。
そのときの内心を点Ｑだとしましょう。
さらに１２０度回転します。
そのときの内心を点Ｒだとしましょう。
すると、内心は、点Ｐ、点Ｑ、点Ｒ　の３箇所だということになってしまいますね。
内心は、１点しかないはずです。
しかし、
コンパスの針の位置そのものを内心だと考えると、内心は１か所、つまり点Ｏが内心だということになり、
内心が１か所しかないことと矛盾しなくなります。

同様の考え方で、重心も点Ｏ（コンパスの針）であることが示せます。


以上、ご参考になりましたら幸いです。

この回答へのお礼

ありがとうございます(＾＾)

1回読んだだけじゃ分からないので
何度も読んで理解をしたいと思います!!

お礼日時：2009/02/25 23:46

No.1 回答者： proto 回答日時： 2009/02/25 19:01

正三角形の内心と"何"が一致するの？

出来るだけわかりやすく補足していただけると嬉しいです。

この回答へのお礼

すいません(＾＾；)
説明が不十分でしたね。

何と一致するのか・・・・？

たぶんなんですが(←え・・・・)
外心、重心となぜ一致するのかだと思うんですよ。
先生が言うのが早かったのであまり聞き取れませんでした；；

わかりますかね？
本当にすみませんでした。
答えてくれると助かります。

回答、ありがとうございます(＾＾)

お礼日時：2009/02/25 19:18