1/xの積分について

1/xを積分するとlogxとなりますが、1/x^2を計算する場合、普通の積分の公式に従って、-x^-1となります。

なぜ1/xのときだけlogxがでてくるのかすごく疑問に思います。

みなさんは疑問に思ったことないでしょうか？

理由知っている方は教えてください。

確かにlogxを微分の定義にしたがってlimなどを使って計算していくと1/xとなり、積分はその逆なんだからlogxとなると言ってしまえばそれですみますが、納得しません。
不思議すぎてたまりません。

この原因はそもそも微分というものが、limという概念で、実際は０ではないが、０とみなしてしまおうという考え方からこのような変な結果がでてきているのでしょうか？

No.10 ベストアンサー 回答者： osn3673 回答日時： 2011/08/29 09:02

> できれば、log(x)がx^0の極限とはどういうことなのか

> 詳しく教えてくれるとありがたいです。

x^0 を x^t の t → 0 の極限として扱うには
実数 t に対する x^t を

　　x^t = exp(t log x)

と考えねばなりません．この場合も

　　dx^t / dx = t x^{t-1}

が成立します．したがって

　　f(x) = (x^t - 1) / t

とおくと，f '(x) = x^{t-1} であり，t ≠ 0
であれば，f(x) をそのまま x^{t-1} の原始関数
として使えます．

t = 0 のときは f(x) = 0 / 0 という不定形に
なるので，ロピタルの定理を使って

　　　lim[t → 0] {(x^t - 1) / t}
　　= (log x) exp(0 log x) / 1
　　= log x

が x^{t-1} の一つの原始関数になります．

参考URL：http://ja.wikipedia.org/wiki/%E3%83%AD%E3%83%94% …

No.9 回答者： osn3673 回答日時： 2011/08/28 17:45

基本的には ANo.7 で解決済みですが，

「log(x)とは，x^0の極限であり，・・・」

には同意しかねます．理由は x^0 の極限 とみなせるのは
x = 1 の近傍に限定されるからです．一般に

　(x^t - 1)/t = (exp(t log x) - 1)/t

は任意の x の近傍で不定形になりますから

「log(x)とは，(x^t - 1)/t の極限であり，・・・」

の方がよいと思います．
蛇足： (x^t)/t も (x^t - 1)/t も原始関数．

この回答への補足

どうも説明ありがとうございました。
ですが、みなさん高度すぎてついていけませんでした。
それほど数学の知識はありませんので。
現在大学生ですが、微積の勉強はやったことありますが、極限の勉強を詳しくやったことがないので、log(x)とは、x^0の極限でありの意味がわかりませんでした。
確か極限ってのはxを０に近づけたときに、log(x)はなにに近づくかでしたっけ？
できれば、log(x)がx^0の極限とはどういうことなのか詳しく教えてくれるとありがたいです。

補足日時：2011/08/29 01:27

No.8 回答者： hiccup 回答日時： 2011/08/27 13:28

No.5 を書いた者です。

後ろめたい気持ちがあって舞い戻ってきました。

No.5 は、たぶん見え方を変えただけです。

別の書き方をすれば、x^n の積分を x^n dx = dy という微分形で書いて、x^n x' = 1 とすれば、n=-1 のときだけ線形になります。微分方程式を解く段階でそこだけが異質なことがわかります。
これが説明になっているのか、単に見方を変えただけなのか、自分ではどちらかわからなくて混乱しています。微分方程式を解くことは積分することですから、そこで堂々巡りが生じていると言われるかもしれません。そこは変数変換によってズバリ解を見つけ、堂々巡りを回避できると思います。

見え方を変えたことで腑に落ちるのならそれもありかなと思うわけですが、そう書いている一方で、理由を説明するということがどういうことかわからなくなっていて、迷宮にいるようです。

No.7 回答者： FT56F001 回答日時： 2011/08/27 10:51

#4の補足です。

#6さんも書いてられますが，log(x)はx^0の極限ですので，
x^nの仲間といえるでしょう。

x^(t-1)の積分はx^t/tです。
積分定数をつけて，x=1で原始関数を0とすると，
∫x^(t-1) dx = (x^t-1)/t
と表せます。ここで，t=0とおくと
(x^0-1)/0となり，0/0の不定形になってしまいます。
極限をとると，

log(x) = lim[t→0] (x^t-1)/t

という表示が成り立ちます。

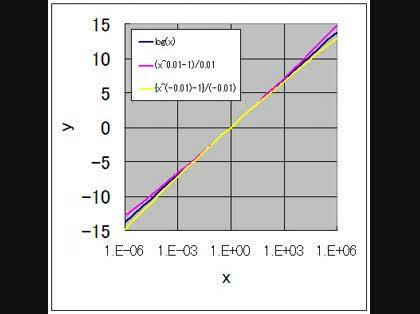
log(x)(青線)，(x^0.01-1)/0.01(赤線)，{x^(-0.01)-1}/(-0.01)(黄線)
を比べてみると，x=10^-3から10^3程度まで，よく一致しています。

このように，
「log(x)とは，x^0の極限であり，べき乗 x^n の仲間だ」
と説明できそうです。

No.6 回答者： hugen 回答日時： 2011/08/26 23:13

∫[1,x]dx/x=logx

∫[1,x]dx/x^(1+t)=(1-1/x^t)/t=(x^t-1)/(t*x^t) →　logx (t→0)

No.5 回答者： hiccup 回答日時： 2011/08/26 17:49

1/x のときだけ仲間はずれになるのは先の回答者が書かれている通りだと思います。

では、なぜ log が出てくるのかといえば、次の理由からですよね。

x=e^y という関数を考えると
dx/dy = e^y
この、微分しても変わらないという性質が肝心ですね。
つまり

dx/dy = x　（← これ）


このあとも書きますと、x は 0 にならないから、あるいは 0 を避けて積分して
∫dx/x = ∫dy = y + C = log x + C

log が出てきました。

No.4 回答者： FT56F001 回答日時： 2011/08/26 10:34

確かに疑問に思いますね。

どうして1/xの積分だけが特殊なのか。

ちなみに，
∫ x^(-0.99) dx =((x^0.01)-1)/0.01
∫ x^(-1.01) dx =(1-(x^(-0.01)))/0.01
∫ x^(-1) dx =log_e(x)
の三つの関数は，x≒1の付近では確かに近い値をとりますね。

log_e(x) = lim [t→0] ((x^t)-1)/t
と表せるわけで，
「べき乗x^nのうち，nが0に近くなった特殊ケースが，
対数log(x)である」
と言えるのかもしれません。

No.3 回答者： girlkeeper 回答日時： 2011/08/26 06:47

（答えになっていませんが）

うーん、分かる分かる。

私の数学経験では、「ｘ^nの積分はｘ^(n+1)／(n+1)」→「じゃあ、ｎ＝－１のときはどうなる？」→「logｘになる」→「ゲ！？」

でした。

演繹的にそうなると言われても、ｎ≠－１のときはただの有理関数になるのに、ｎ＝１のときだけ突拍子も無い　logｘ　になるのは直感的に納得がいかない。

個人的には、積分が区分求積の「無限和」で表されるってところがミソなんだと理解しています。
無限に足すなら何でもアリなんだろうと。　３＋０．１＋０．０４＋・・・はπになるしｗ。

ただ、そうなると逆に、ｎ≠－１のときに単純な関数になる方が不思議になってきたりする。積分って奥深い。

（蛇足）私は１／（ｘ^2＋１）の積分の方が好きです。

No.2 回答者： alice_44 回答日時： 2011/08/26 01:07

べき乗の微分を習ったとき、(d/dx) x^n = n x^(n-1) は

n = 0 の場合だけ成り立っていなかったんだけど、
積分するまで、変に思わなかったの？

No.1 回答者： DJ-Potato 回答日時： 2011/08/26 00:53

x^nを積分すると

1/(n+1)・x^(n+1)
になります。

この時、1/xではn=-1ですから、1/(n+1)=1/0になります。

積分に限らず、数学では一般式で分母が0になるような時は特別扱いなんです。
逆に言うと、積分に関して、1/xはx^2や1/x^2やx^5の仲間ではないのです。
1/xはx^nではないのです。

それはもう、数学の基礎の基礎で、偉い学者さんが頭を悩ませて導き出したもので、我々常人が踏み込む領域ではないのかもしれません。