くじ引きの確率

5本のうち、あたりが2本はいっているくじがあります。このくじをAが先にひいて、箱に戻し
Bがひきます。
問題
A,Bともにはずれをひく確率を求める

この問題で疑問があるのですが、A,Bともにはずれをひくことは、全体１からA,Bともに当たりをひく確率を引けば答えが出るのではないですか？
この方法で答えを出すと間違った答えがでます。
この方法のどこが間違っているのか教えてください。

No.1 ベストアンサー 回答者： shuu_01 回答日時： 2013/12/17 00:52

A がはずれをひく確率は 3/5、B もはずれをひく確率は 3/5

A も B もはずれ をひく確率は (3/5)^2 ＝ 9/25 ＝ 36% です

A があたりを引く確率は 2/5、B もあたりをひく確率は 2/5

A も B もあたりをひく各私立は (2/5)^2 ＝ 4/25 ＝ 16% です

それ以外の確率は

A がはずれをひいて、B があたりをひく確率の (3/5） （2/5）
= 6/25 ＝ 24%

A があたりをひいて、B がはずれをひく確率の (2/5) (3/5）
= 6/25 ＝ 24%

で全部 合わせると 36 + 16 + 24 + 24 = 100% でぴったりです

＞　A,Bともにはずれをひくことは、
＞　全体１からA,Bともに当たりをひく確率を引けば
＞　答えが出るのではないですか？

一人があたりで、もう一人がはずれを忘れちゃいけません

この回答へのお礼

回答ありがとうございます。
理解できました。

お礼日時：2013/12/17 21:50

No.3 回答者： naniwacchi 回答日時： 2013/12/17 02:45

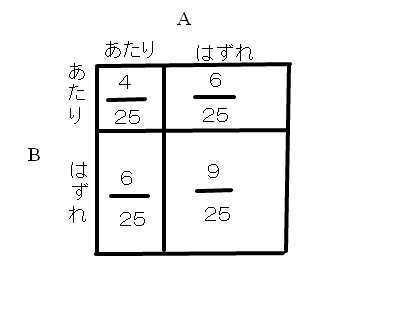
単に Aと Bのあたり・はずれだけに注目すると、

1) Aがあたり、Bもあたる
2) Aがあたり、Bははずれる
3) Aがはずれ、Bはあたる
4) Aがはずれ、Bもはずれる

の 4とおりの組合せがあります。求めたい確率は 4)です。
質問者さんの方法では、全体から 1)を引くことしか考えていません。
よって、2)や 3)の確率も含まれてしまいます。

この回答へのお礼

回答ありがとうございます。

お礼日時：2013/12/17 21:51

No.2 回答者： asuncion 回答日時： 2013/12/17 01:16

別の回答者からの回答のとおり、

2人ともはずれ
の余事象は
2人とも当たり
「ではありません」

この回答へのお礼

回答ありがとございます。
理解できました。

お礼日時：2013/12/17 21:51