三角比について(青チャート1A例題138) 三角方程式を解く時はsinθ＝y, cosθ＝x tan

三角比について(青チャート1A例題138)
三角方程式を解く時はsinθ＝y, cosθ＝x
tanθ＝y/xと置いて
参考書に写真の単位円の図形を埋め込むと書いてました。
なのでsinθ＝1/√2の時　y＝1/√2
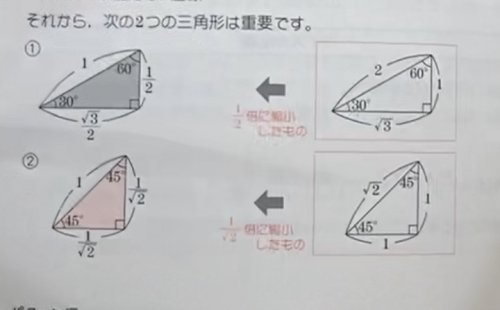
なので縦の長さが1/√2の②の図形を埋め込むと補足画像のようになりθが45°,135°になると参考書には載ってました
しかしtanθ＝-1/√3の時x＝√3,y＝-1なので
縦が1横が√3の三角形を埋め込むと思ったのですが
そのような三角形は①にも②にもありません
tanθは単位円で考えれないのですか？

質問者からの補足コメント

• 補足画像

  
    補足日時：2020/11/16 17:51

No.6 回答者： ゼロプライム 回答日時： 2020/11/16 20:57

単位円の円周上の点をP(x , y) 、OPとx軸の正の部分とのなす角をθ とすると、

cos θ=x
sin θ=y
tan θ=y/x
となります。
sin θ=1/√2 のとき、y=1/√2 なので②の図形をはめ込むことができ、θ＝45°、135°となります。

tan θ= - 1/√3 のとき、x＝√3、y＝-1とするとP(√3 , -1) は単位円の円周上の点ではないのでうまくいきません。tan θ=y/x ですが、ｘとｙを別々に考えるのではなく、y/x のまま考えます。y/x はOとPを結ぶ直線の傾きです。傾きが - 1/√3 と考えると①の図形をはめ込むことができ、θ＝150°、330°となります。

No.5 回答者： ありものがたり 回答日時： 2020/11/16 20:39

直角三角形を使って考えると、

角度が 0°〜90° の範囲の三角比しか考えることができません。
その範囲でしか、直角三角形が作れないからです。

0°〜360° の範囲の三角関数を考えるためには、直角三角形ではなく
単位円を使って考えましょう。
x軸の正部分を、原点中心反時計回りに θ 回転した半直線と
単位円との交点の座標を (cosθ,sinθ) とするのです。

中学では、直角三角形を使って三角比を定義しますが、
高校では、単位円を使って三角関数を定義します。
このやり方に慣れてゆく必要がありますね。

tanθ = -1/√3 を表す単位円上の (x,y) には
(x,y) = (-1/2, √3/2), (1/2, -√3/2) のふたつがあります。
(-1/2, √3/2) は θ = 150° に、
(1/2, -√3/2) は θ = 330° に対応しています。

このふたつの角度は、補足の説明文で見切れている
単位円に直角三角形を「はめこむ」考え方で、
180° - 30° = 150°,
150° + 180° = 330° と計算して見つけることができます。
ことのき、①の図から 30° が出てくるのです。

No.4 回答者： finalbento 回答日時： 2020/11/16 20:06

恐らく質問者様は単位円の定義である「半径の長さが1の円」と言う意味を誤解していると思います。

「半径の長さが1」と言うのは「半径が1cm」「半径が1m」と言う具合に半径の長さの数値を問題にしているわけではなくて「半径の長さを1と考えた円」と言う意味です。なので①の右側の直角三角形を単位円で考えるなら例えば「長さ2cmの斜辺の長さを1に取る」と言う事ですから、もちろん単位円で考える事ができます。

No.3 回答者： むらさめ 回答日時： 2020/11/16 19:46

下の図はθの範囲が180°まで限定されていますが、覚えるとしたら360°まで覚えないといけないです

tanθ＝-1/√3の時　x＝√3,y＝-1　←　それ故にこれはすこし足りないです
tanθ＝-1/√3の時は、x＝√3,y＝-1　と　x=-√3,y=1　の時も考えないといけないです。

上図①の三角形を応用して考えるか、あるいは暗記しないといけないレベルのことです。
x=-√3,y=1　は単位円1なら　第二象限　θ=150°　x=-√3/2,y=1/2　tanθ=-√3/3
x＝√3,y＝-1　は単位円1なら　第四象限　θ=330°　x=√3/2,y=-1/2　tanθ=-√3/3

三角関数　sin　cos　tan　が30°刻み45°刻みでどの値を取るのかは、単位円が頭の中にすぐに浮かんで、値が出てくるようにして置かなければ試験で勝負にならないです。これは何が何でも”絶対”です。
必要なら、三角関数のグラフを雑でいいので、何度も書いて頭の中に叩き込むくらいしてもいいです。

No.2 回答者： finalbento 回答日時： 2020/11/16 19:19

「縦が1横が√3の直角三角形」と言うなら①だと書いてありますよ。

現に①の右側の図の直角三角形はズバリそうなっていますし、それを1/2倍したものが①の左側の直角三角形になっています。そもそも「縦が1横が√3」などと言うのは辺同士の比だけが問題なので、例えば「縦が1/2cm、横が√3/2cm」となっていても同じ事です。

この回答へのお礼

もし1の右側の図形を使うのであれば単位円では求めれないということでしょうか？

お礼日時：2020/11/16 19:37

No.1 回答者： むらさめ 回答日時： 2020/11/16 18:15

tanも基本は単位円で考えます。

添付の画像でそのような記述がされていないだけです。
編集の都合と言っても良いかもしないです。

tanθ=sinθ/cosθ=y/x　で合っていますよ。

この回答へのお礼

しかしtanθ＝-1/√3の時x＝√3,y＝-1なので
縦が1横が√3の三角形を埋め込むと思ったのですが
そのような三角形は①にも②にもありません
→このような場合どのように考えればいいのでしょうか？

お礼日時：2020/11/16 18:54