閉曲線の向きの判定法

閉曲線の向きの判定法


平面上に交差していない１本の閉曲線があります。
この閉曲線上の座標点配列がちょうど１周分与えられている

　(x0,y0),(x1,y1),(x2,y2), ... (xn,yn)

とき、この座標配列の向きが時計回りになっているか
反時計回りになっているかを判定する方法を教えてください。

No.2 ベストアンサー 回答者： nag0720 回答日時： 2010/01/05 11:17

点(x0,y0),(x1,y1),(x2,y2),...,(xn,yn)に対し、

S=Σ[i=0...n](xiy(i+1)-x(i+1)yi)　　（但し、x(n+1)=x0, y(n+1)=y0）
=(x0y1-x1y0)+(x1y2-x2y1)+...+(xny0-x0yn)
とするとき、
S＞0なら反時計回り、S＜0なら時計回りです。

なお、|S/2|はそれらの点でできる多角形の面積を表します。

この回答へのお礼

ありがとうございました。
大変役立ちました。

お礼日時：2010/01/08 11:19

No.3 回答者： alice_38 回答日時： 2010/01/05 17:32

閉曲線が、自己交差を持たないようなものであれば、

♯1 の図の場合も含めて、
♯2 の方法で、曲線の向きを定義できます。
サンプル点の座標だけでなく
曲線の媒介変数表示が与えられていれば、
Σでなく∫でやるんですがね。

自己交差してしまうと、
例えば ∞ のような形の曲線だと、
「向き」が定義できるかどうか
問題になるでしょうが。

No.1 回答者： graycat000 回答日時： 2010/01/05 11:14

その閉曲線は凹みのない曲線，円や楕円のような形状でしょうか？

そうであれば微分値を計算してその変化の具合を見ればよいでしょう．

(x'(n),y'(n)) = ({x(n+1)-x(n)}, {y(n+1)-y(n)})

を計算してその変化の具合を見ます．

nを0からnまで追っていき，(x'(n),y'(n))のx'(n)かy'(n)の符号が変化する点（円に外接する長方形との接点）の符号変化が

「x'(n)が-から+」→「y'(n)が+から-」→「x'(n)が+から-」→「y'(n)が-から+」
のパターンに同一ならば時計回り，

「x'(n)が-から+」→「y'(n)が-から+」→「x'(n)が+から-」→「y'(n)が+から-」
のパターンに同一ならば反時計回りです．

要するに，円の最左点，最高点，最右点，最低点を基準点としてそれらをどう回るかをチェックします．

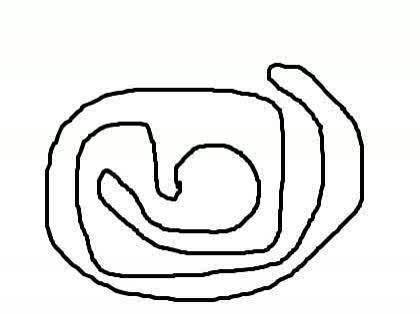
ちなみに，添付した画像のような曲線も閉曲線ですが，こんな曲線も許す任意の閉曲線の場合は「そもそも任意の閉曲線上の時計回りとはなんなのか？」という定義をきちんと示す必要があります．
添付画像の線をどの方向に追ってもこれは時計回りか反時計回りか悩むと思います．