図形と計量

数学の図形と計量の問題です。
分かる方がいたら教えて下さい!
ちなみに私は高２なので、高２で解ける
範囲でお願いします。


.

問.傾斜が30°で一定の坂の頂上に塔が立っている。坂のふもとからこの塔の先を見ると、水平面に対して45°の角度に見えた。坂を斜面に沿って塔に向かって30m進んだA点から再び塔の先を見ると、水平面に対して60°の角度に見えた。

(1)A点から坂の頂上まで、斜面に沿ってさらに何mあるか。

(2)塔そのものの高さは何mであるか。

(3)塔の先と坂のふもとの高低差は何mあるか。


ちなみに答えは、
(1)10√3m
(2)10√3m
(3)15√3+15m
になります。


今日中にお願いします!!!
考え方だけでなく、途中式も出来るだけわかりやすく
細かくお願いします!!

注文が多くてすみません。
宜しくおねがいします。

No.1 回答者： noname#157574 回答日時： 2012/07/05 23:49

図をかきなさい。

この回答への補足

図を書いたのですが、どこからどう手をつけていいのか分かりません…。
この範囲は苦手なので…。
ホントに困っています。
途中式を教えていただけませんか？
お願いします。

補足日時：2012/07/06 00:04

No.2 回答者： noboundly 回答日時： 2012/07/06 01:24

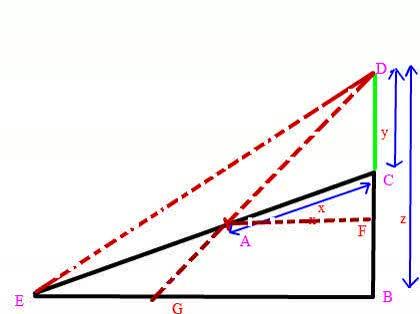
図のように三角形EBC、塔CD、点F,Gをとり、

AC=x, CD=y, BD=z　とする。
また問題文より、AE＝30

∠DEB＝45°,∠B＝90°　より、
BE=z=(30+x)cos30°・・・(1)
∠CAF＝30°より、∠DAC＝60°-30°＝30°
∠DGB＝60°より、∠ADF＝30°
よって、∠ADF＝∠DAC　だから　x=y・・・(2)

(30+x)sin30°+y=z ・・・(3)(←BC+y=z）

(1)(2)(3)をといて　x=10√3, y=10√3, z=15+15√3

No.3 回答者： wild_kit 回答日時： 2012/07/06 09:35

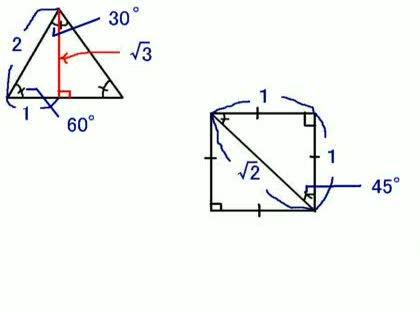
　添付画像のように、直角二等辺三角形（右下）の辺の比率は１：１：√２であり、３０°、６０°、９０°であれば、２：１：√３になります。

　斜面の長さをｘとします。
すると坂のふもとから坂の頂上までの水平距離は、｛（√３）ｘ｝／２、高低差はｘ／２です。
ふもとから塔の先までの角度が４５°ということですから、その高低差は水平距離と同じ｛（√３）ｘ｝／２です。
すると、塔の高さは［｛（√３）ｘ｝／２］－（ｘ／２）　＝　［｛（√３）－１｝ｘ］／２

　斜面を３０ｍ上がると、塔の先までの角度が６０°になります。
Ａ点から坂の頂上までの水平距離は√３（ｘ－３０）／２、高低差は（ｘ－３０）／２です。
Ａ点と塔の先までの高低差は、√３｛√３（ｘ－３０）｝／２　＝　３（ｘ－３０）／２
塔の高さは、｛３（ｘ－３０）／２｝－｛（ｘ－３０）／２｝　＝　ｘ－３０

どちらも同じ等の高さだから、［｛（√３）－１｝ｘ］／２　＝　ｘ－３０
｛（√３）－１｝ｘ　＝　２ｘ－６０
｛（√３）－１－２｝ｘ　＝　－６０
（－３＋√３）ｘ　＝　－６０
ｘ　＝　－６０／（－３＋√３）　＝　｛－６０（－３－√３）｝／｛（－３＋√３）（－３－√３）｝
＝　｛－６０（－３－√３）｝／（９－３）　＝　－１０（－３－√３）　＝　３０＋１０√３
斜面の長さｘ＝３０＋１０√３＜ｍ＞

（１）Ａ点から頂上までは、３０＋（１０√３）－３０　＝　１０√３＜ｍ＞
（２）塔の高さは、３０＋（１０√３）－３０＝　１０√３＜ｍ＞
（３）塔の先とふもとの高低差は、｛（３０＋１０√３）／２｝＋１０√３　＝１５＋１５√３＜ｍ＞
（ふもとから頂上までの高低差は、斜面の長さの１／２だから、それに塔の高さを加えると求まる。）

No.4 回答者： yyssaa 回答日時： 2012/07/06 17:13

図が描けたら、次の手順で進めます。

まず、A点から坂の頂上まで、斜面に沿ってさらにxmあるとして、
坂のふもとを基準にA点及び坂の頂上の水平距離及び高低差を
求めます。
・坂のふもととA点の水平距離は、「傾斜が30°で一定の坂」
なので30cos30°=30*{(√3)/2}(m)・・・・・・・・・・・・・・・・・・・・・・・・(ア)
・坂のふもとと坂の頂上の水平距離は、同様に(30+x)cos30°
=(30+x){(√3)/2}(m)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(イ)
・坂のふもととA点の高低差は、30sin30°
=30*(1/2)=15(m)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(ウ)
・坂のふもとと坂の頂上の高低差は、(30+x)sin30°
=(30+x)(1/2)=(30+x)/2・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(エ)
　次に塔の先の位置を計算します。
「坂のふもとからこの塔の先を見ると、水平面に対して45°
の角度に見えた」ので、坂のふもととこの塔の先の高低差は、
この塔が立っている坂の頂上と坂のふもとの水平距離に等しく
なります。よって、(イ)より
坂のふもととこの塔の先の高低差=(30+x){(√3)/2}(m)・・・・・・・(オ)
　また、「A点から再び塔の先を見ると、水平面に対して60°の
角度に見えた」ので、A点とこの塔の先との高低差は、A点と
この塔が立っている坂の頂上との水平距離)×tan60°になり、
この水平距離は、(イ)ー(ア)=(30+x){(√3)/2}-30*{(√3)/2}
=x(√3)/2なので、A点とこの塔の先との高低差はx{(√3)/2}√3
=3x/2(m)となり、これに坂のふもととA点の高低差を加えると、
坂のふもととこの塔の先との高低差になるので、(ウ)より
坂のふもととこの塔の先の高低差=(3x/2)+15(m)・・・・・・・・・・・・・(カ)
が得られます。
　以上で2地点(坂のふもととA点)から見た塔の先の位置が計算
出来たので、(オ)=(カ)としてxを求めると
(30+x){(√3)/2}=(3x/2)+15よりx=10√3となります。
よって、

(1)A点から坂の頂上まで、斜面に沿ってさらに何mあるか。
この距離をx(m)としたので、10√3(m)・・・答え

(2)塔そのものの高さは何mであるか。
(カ)とx=10√3から
坂のふもととこの塔の先の高低差=(3x/2)+15=(3*10√3)/2+15
=15√3+15
(エ)とx=10√3から
坂のふもとと坂の頂上の高低差=(30+x)/2=(30+10√3)/2=15+5√3
塔そのものの高さは(坂のふもととこの塔の先の高低差)マイナス
(坂のふもとと坂の頂上の高低差)なので、
15√3+15-(15+5√3)=10√3(m)・・・答え

(3)塔の先と坂のふもとの高低差は何mあるか。
(2)の計算過程から15√3+15(m)・・・答え