質点系の角運動量

両端に質量ＰとＱがとりつけられた長さ２ｌの重さの無視できる棒の中央Ｏの周りの力のモーメントＮを求めよ。

解き方がわかりません。
教えてください。

No.5 回答者： hitokotonusi 回答日時： 2013/07/14 21:04

外力というのは重力なんでしょうね。

まあ、だいたい何をしたいのかはわかりました。
おそらくは重心運動と重心まわりの運動の分離なんでしょうね。

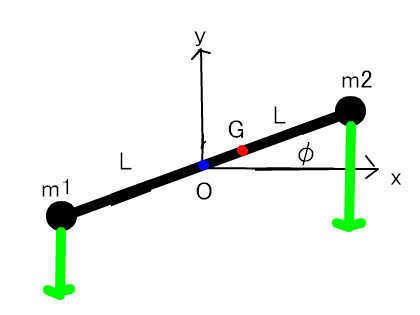
添付図の設定で、Oからm1, m2までの水平距離(これが腕の長さに等しい)がL cosφなので、
モーメントは反時計回りを正として

N = m1 g L cosφ- m2 g L cosφ= (m1 - m2) g L cosφ

Oを原点として重心のX座標は X = (- m1 L cosφ + m2 Lcosφ) / (m1 + m2) = Lcosφ (m2-m1)/(m1+m2)

重心はその定義から力の逆比で内分する点で、
重力の場合は力が質量に比例するので質量の逆比で内分する点。
したがって、重心からの各質点の重力への腕の長さをd1, d2とすると

d1 : d2 = m2 : m1

したがって重心まわりのトルクN'は

N' = m1 g d1 - m2 g d2 ～ m1 g m2 - m2 g m1 = 0

重心の位置に質量m1+m2の質点があるとするとこのトルクは、Xが正の時マイナスのトルクを与えるので

Ng = - (m1+m2)g X = - (m1+ m2) g Lcosφ (m2-m1)/(m1+m2) = (m1-m2) g Lcosφ

以上より、

N = Ng + N'

この先はおそらく・・・・・・・

剛体のOを中心とする慣性モーメントをI, 重心Gを中心とする慣性モーメントをI’とすると、
OとGの距離をdとして平行軸の定理から

I = I’ + Md^2

剛体の角加速度はどこを中心としても同じなので、角加速度をαとして、O点まわりの運動方程式は

I α = N

これに上の結果を代入すると

(I' + Md^2) α = N' + Ng

ここでMd^2は重心の位置にある質量Mの質点の慣性モーメントで、I', N'はいずれも重心を回転中心とする時の量である事を考えると、それぞれ

重心まわりの運動方程式　I' α = N'
重心にある質点の運動方程式　(Md^2) α = Ng

と、重心の運動と重心まわりの運動に分離できる

・・・・・・というような説明が続くと思われます。

No.4 回答者： tknakamuri 回答日時： 2013/07/14 13:59

>力がすべて重心に集まったと想定

重力の話？？？？

>外力
また新しい力が登場？？？？？

ますます意味不明に磨きがかかってます(^^;

No.3 回答者： uen_sap 回答日時： 2013/07/13 15:57

？？？

情報不足、力は重力 or 別？
重力として棒は垂直、水平 or ある角度を持っている？

この回答への補足

情報不足でした。
すいません。

問題文の続きです。

ただし、質点Ｐ、Ｑの質量をｍ１、ｍ２、重力加速度をｇとし、
力がすべて重心に集まったと想定したときの
点Ｏの周りの外力のモーメントＮｇ、及び重心の周りの外力のモーメントＮ’としたとき
Ｎ＝Ｎｇ＋Ｎ’が成り立つことを示せ。

と書いてありました。

あと傾きφに傾いています。

補足日時：2013/07/13 17:10

No.2 回答者： hitokotonusi 回答日時： 2013/07/13 15:15

力のモーメントですか？

どんな力がどのように働いているのか書いないので、解答不能です。
仮に重力としても、水平か傾いているのかで答えがちがいます。

この回答への補足

情報不足でした。
すいません。

問題文の続きです。

ただし、質点Ｐ、Ｑの質量をｍ１、ｍ２、重力加速度をｇとし、
力がすべて重心に集まったと想定したときの
点Ｏの周りの外力のモーメントＮｇ、及び重心の周りの外力のモーメントＮ’としたとき
Ｎ＝Ｎｇ＋Ｎ’が成り立つことを示せ。

と書いてありました。

補足日時：2013/07/13 17:09

No.1 回答者： hitokotonusi 回答日時： 2013/07/13 11:57

角運動量関係ないですね。

一つの質点の慣性モーメントは

(質量)×(回転軸からの距離)^2

複数の質点が含まれている質点系の場合、全ての質点についてモーメントの総和をとる。

この回答への補足

慣性モーメントはおっしゃる通り求めれますが
この問いは力のモーメントなのですが。

補足日時：2013/07/13 15:02