Q3を教えてください

Q3を教えてください

No.1 ベストアンサー 回答者： masterkoto 回答日時： 2019/02/04 11:37

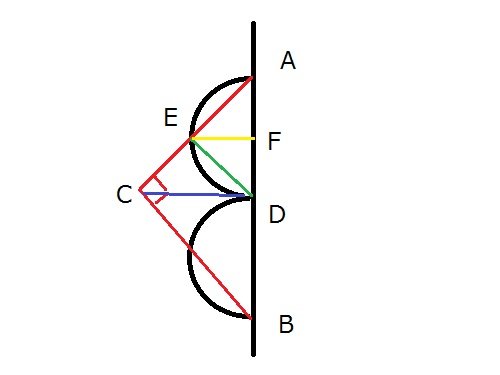
Lを軸に回転するので、直角2等辺三角形の位置が下図の赤線の位置にあっても、でき上がる立体の形は問題の画像のものと同じです。

そこで、赤線の位置に直角2等辺三角形を移動させた状態で考えます。
次にABの中点と直角2等辺三角形の頂点を青線で結びます。
直角2等辺三角形の頂点から対辺の中点におろした線分だから青線はLに垂直です。
つまり青線はABの中点の垂直二等分線！
図形の対称性から、下図は青線を境にして2つに切ると全く同じ形になります
（△ACD合同△BCD)
だから、以下△ACDの事だけを考えます
ACと半円の交点をEとすると半円の直径ADに対する円周角だから、∠AED=90度
∠EAD=45°（△ACDは直角2等辺三角形だから）
従って△AEDも直角2等辺三角形です
次に、直角2等辺三角形の頂点EからADに垂線（黄色）をおろすとこれはADを2等分します
つまり、EFはADの垂直二等分線！
これらをまとめると、△ACDは∠CDA=90の直角2等辺三角形
△AEFは∠EFA=90の直角2等辺三角形
EF//CDです！！
　
さて準備ができたので回転してできる立体を考えます。
求める立体の上半分の姿は、台形CDFEを回転したものと、扇形AEFを回転したものを合わせた物になります。
扇形AEFを回転してできるものは半径１の球の上半分です。（AB=４、AD=２、AF=1)
したがって球の体積の公式
球の体積=4xΠx(半径)³/3「語呂合わせ：身の上に心配あるの参上]
でその体積が求まります！
次に台形CDFEを回転してできる立体について、
これは△ACDの回転体から△AEFの回転体を取り除けばよいのです
△ACDの回転体は半径CD高さADの円錐（△ACDは直角2等辺三角形でCD=AD=2)
△AEFの回転体は半径EF高さAFの円錐（△AEFも直角2等辺三角形でEF=AF=1)
なので2つの円錐の面積を求めれば、
台形CDFEを回転した立体の体積＝大きい円錐-小さい円錐
が求まります。
これで求める立体の上半分の体積が分かるので、2倍すれば答えです＾－＾

No.3 回答者： ほい3 回答日時： 2019/02/04 12:03

読み返して、文章がわかりにくいので、上の2行訂正。

回転した立体の上半分は高さ2の円錐の底から1の部分と
半径1の半球から出来ている。
円錐の部分は大きな円錐－小さな円錐で求められる。

この回答へのお礼

ありがとうございます。
甲乙付けがたい回答をいただけたのですが、今回は最後まで補助輪を外さないでお答えしてくれたNo.1さんをベストアンサーにさせていただきます。

お礼日時：2019/02/04 12:07

No.2 回答者： ほい3 回答日時： 2019/02/04 11:50

回転した立体の上半分は高さ2の円錐の底から1の部分で

大きな円錐－小さな円錐で求められる。
また、上は半径1の半球（4πｒ³/3）となるので、合せると
（大きな円錐底面は半径2高さ2、小さな方は半径1高さ1のため、
円錐堆積πr²ｈ/3から）
π2²・2/3-π1²・1/3+4π・1³/3/2＝8π/3-π/3+2π/3＝9π/3＝3π
これが、上半分なので、全体は2倍の、6π（ｃｍ³）

どうでしょうか？