確率密度関数です。

確率密度関数です。

途中からなんだかおかしくなってきていまして、、
まず（１）からできていのかなと


すみませんがお詳しい方よろしくお願いいたします

No.1 回答者： kamiyasiro 回答日時： 2022/04/05 09:31

手計算でも出来ますが、こんな問題はコンピュータを使わないと大変ですよ。

授業ではエクセルかRかPythonで説明があったのではないですか？

(1)は定積分して面積を１にするようにｋを決めるのだけど、ソルバーで解いた方が早い。 →　ｋ＝1/4

(5)は、１次の積率と２次の中心積率の問題だけど、f(x)で数値が与えられれば、それから求めた方が良いかも。

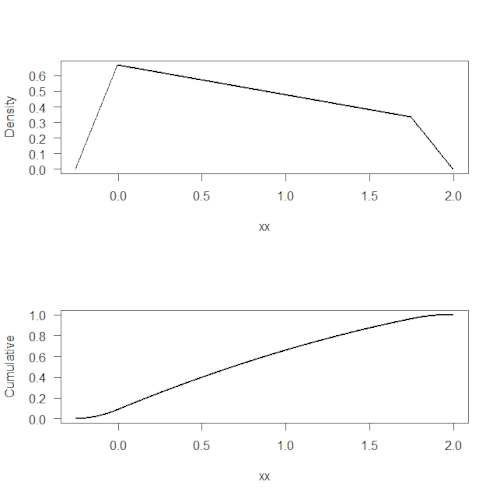
グラフは、特にF(x)は曲線になるからコンピュータでないと描けないです。

解を投稿するのはめちゃめちゃ面倒なので、グラフだけアップしておきます。

ご参考まで。

No.2 回答者： yhr2 回答日時： 2022/04/05 10:29

おそらく、(1) ができないので全滅なのでしょうね。

(1) 「確率密度」ですから、全範囲で積分すれば合計確率は 1 にならないといけません。

従って
　∫[-k→0][(2/3k)x + 2/3]dx + ∫[0→7k][-(1/21k)x + 2/3]dx + ∫[7k→8k][-(1/3k)x + 8/3]dx = 1
→　[(1/3k)x^2 + (2/3)x][-k→0] + [-(1/42k)x^2 + (2/3)x][0→7k] + [-(1/6k)x^2 + (8/3)x][7k→8k]
= -(1/3)k + (2/3)k - (7/6)k + (14/3)k - (32/3)k + (64/3)k + (49/6)k - (56/3)k
= 4k
なので
　k = 1/4

(2) ということは
　f(x) = 0 (x < -1/4)　　　　　　　　　　　①
　　　= (8/3)x + 2/3 (-1/4 ≦ x ≦ 0)　　　　②
　　　= -(4/21)x + 2/3 (0 ≦ x ≦ 7/4)　　 　③
　　　= -(4/3)x + 8/3 (7/4 ≦ x ≦ 2)　　　　④
　　　= 0 (2 < x)　　　　　　　　　　　　　⑤

この y = f(x) のグラフは書けますね？

(3) 変数の範囲は
　-1/8 < x < 1/4
ですから、②と③の範囲内です。
区間を2つに分けて積分すれば求まります。

(4) 変数の範囲は
　1 ≦ x
ですから、④と⑤の範囲内です。
④の範囲だけを積分すれば求まります。

(5) 期待値の定義は、各々の積分範囲全体で
　E[X] = ∫x･f(x)dx　　　⑥

分散は
　V[X] = E[X^2] - {E[X]}^2
の公式を使って求めるのが簡単かな。（公式の導出は一生に最低一度は自分でやってみること）
⑥と同様に
　E[X^2] = ∫x^2･f(x)dx
です。

(6) 分布関数は「-∞ からの累積確率」の関数です。
　F(x) = ∫[-∞→x]f(t)dt

No.3 回答者： kamiyasiro 回答日時： 2022/04/06 13:30

Rでやってみた系の回答です。

Rユーザーでなければ、何のことか意味不明でしょうが、スクリプトを載せておきます。
次のように計算結果が出ました。

(3)の確率は、0.2232143
(4)の確率は、0.3452381
(5)期待値は、0.75．分散は、0.3229156

手計算でやると分数で出てくるかもしれませんね。こっちは小数になっていますので、答え合わせに使って下さいませ。


> # 教えてgooの確率問題
> rm(list = ls())

> par(ask =T)
> par(mfrow = c(2, 1))

> # 確率密度関数を定義する

> fx <- function(x){
+ if(-K <= x && x < 0) y <- 2/3 * 1/K * x + 2/3
+ if( 0 <= x && x < 7 * K) y <- -1/21 * 1/K * x + 2/3
+ if(7 * K <= x && x <= 8 * K) y <- -1/3 * 1/K * x + 8/3
+ return(y)
+ }

> # 損失関数を定義する

> loss <- function(k){
+ K <<- k
+ s1 <- integrate(fx, lower = -k, upper = 0)$value
+ s2 <- integrate(fx, lower = 0, upper = 7 * k)$value
+ s3 <- integrate(fx, lower = 7 * k, upper = 8 * k)$value
+ s <- s1 + s2 + s3
+ return((s - 1)^2)
+ }


> k <- optimize(loss, c(0, 5), tol = 0.001)
> k$minimum
[1] 0.25

> k <- k$minimum
> d <- k / 100
> xx <- seq(-k, 8 * k, by = d)
> yy <- NULL

> # 以下のグラフは以前投稿済み

> for(x in xx){
+ yy <- append(yy, fx(x))
+ }

> plot(xx, yy, las = 1, cex = 0.1, ylab = "Density")
> plot(xx, cumsum(yy * d), las = 1, cex = 0.1, ylab = "Cumulative")

> s <- sum(yy) * d
> s
[1] 1


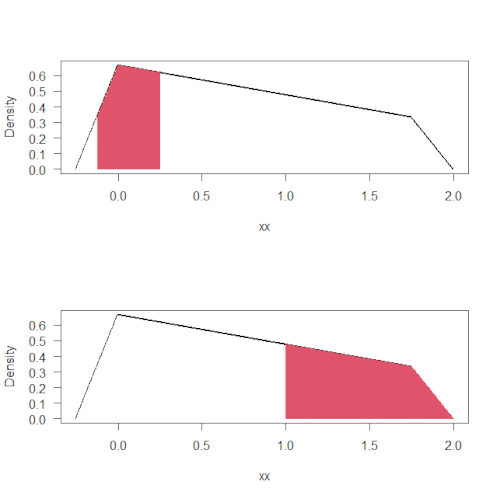
> # P(-1/2 * k <= x && x < k)
> s4 <- integrate(fx, lower = -1/2 * k, upper = 0)$value
> s5 <- integrate(fx, lower = 0, upper = k)$value
> s4 + s5
[1] 0.2232143

> plot(xx, yy, las = 1, cex = 0.1, ylab = "Density")
> index1 <- which(xx == -1/2 * k)
> index2 <- which(xx == k)
> for(i in index1:index2){
+ lines(c(xx[i], xx[i]), c(0, fx(xx[i])), col = 2)
+ }

> # P(4 * k < x)
> s6 <- integrate(fx, lower = 4 * k, upper = 7 * k)$value
> s7 <- integrate(fx, lower = 7 * k, upper = 8 * k)$value
> s6 + s7
[1] 0.3452381

> plot(xx, yy, las = 1, cex = 0.1, ylab = "Density")
> index1 <- which(xx == 4 * k)
> index2 <- which(xx == 8 * k)
> for(i in index1:index2){
+ lines(c(xx[i], xx[i]), c(0, fx(xx[i])), col = 2)
+ }

> # 期待値
> m <- sum(xx * yy) * d
> m
[1] 0.75

> # 分散
> v <- sum((xx - m)^2 * yy) * d
> v
[1] 0.3229156
> sum(xx^2 * yy) * d - m^2 # 分散の公式でも同じ
[1] 0.3229156