No.1ベストアンサー
- 回答日時:
任意の2つの合同な△ABCと△A'B'C'に対して、一方を他方に
移す変換を考えれば十分です。
1. △ABCと△A'B'C'とが裏返ししないと重ならない場合は任意の
直線について1回対称移動します
2. △ABCと△A'B'C'が回転と平行移動だけで重なり、裏返しの
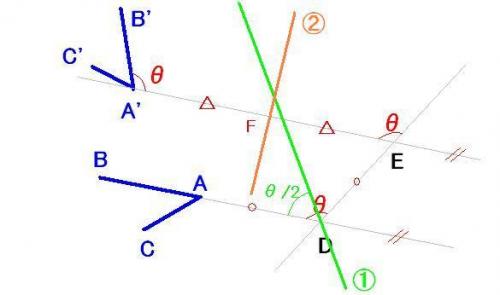
必要がない場合は図のようにします
a) BAを延長した直線を引く
b) a)の直線にに並行でA'を通る直線を引く
c) b)の直線上の点E、a)の直線上の点Dを、∠EDA=∠B'A'Eと
なるように取る
d)∠ADEの二等分線(1)について対称移動
e)A'Eの垂直二等分線(2)についての対称移動
以上より、
裏返しが必要な場合は1.とd)e)で3つ以内、
裏返しが必要ない場合はd)e)で2つ以内
の対称変換の合成になります。
お探しのQ&Aが見つからない時は、教えて!gooで質問しましょう!
似たような質問が見つかりました
- アンテナ・ケーブル 家屋テレビ用アンテナ配線 4 2023/04/27 15:00
- 物理学 時間の進み方が変化する場合、スケール効果を考えるのは当然では? 1 2022/04/18 07:46
- 数学 3次元実ベクトル空間において, 平面 P:x-y+z+1=0 と直線 L:2(x-1)=-y=-z 3 2022/10/29 14:39
- 統計学 加重最小二乗法=①「変数を自然対数変換」=②「誤差項の分散の逆数を重み付け」? 8 2022/11/26 11:15
- Excel(エクセル) Excelシフト表 固定シフトの自動変換化 1 2022/04/14 16:10
- 数学 フーリエ変換後の負の周波数成分の扱いについて 4 2022/09/03 10:18
- ノートパソコン PCからテレビへHDMI 映像は飛ぶけど音声が飛ばない 9 2023/08/22 11:13
- ファンタジー・SF 映画『サマータイムマシンブルース』題名はハッブルの後継機JWの性能のみならず4/19の津波を話題に? 1 2023/04/06 16:07
- 哲学 美大に通っている者です。美術関係の哲学を履修しています。 最近に出た課題の小テストについて、どれが正 2 2022/07/09 22:45
- 物理学 アインシュタイン博士の相対性理論は間違っていたのでしょうか? 6 2022/04/13 17:36
おすすめ情報
デイリーランキングこのカテゴリの人気デイリーQ&Aランキング
-
メール文章で直線の描き方について
-
PowerPoint 罫線で直線を引く...
-
円x²+y²=1と直線y=x+mが接する...
-
三角形の辺の和が最小になるよ...
-
平面ベクトルの方程式について
-
2直線を含む平面
-
三次元ユークリッド空間上の直...
-
線形計画法の解法について!
-
平行条件には2直線が一致する...
-
2直線が交わるかどうかの判定式...
-
相関係数と回帰直線ってなんで...
-
指数近似曲線の計算方法について
-
general formとstandard formの...
-
ベクトルの終点と存在範囲で、O...
-
数学『積分』 2つの曲線の間の...
-
1997年センター試験(追)の...
-
数学Ⅱ 直線の方程式を求めよと...
-
直線を含む平面
-
初歩的な質問で申し訳ないので...
-
数学の場合分けの番号振り
マンスリーランキングこのカテゴリの人気マンスリーQ&Aランキング
-
メール文章で直線の描き方について
-
PowerPoint 罫線で直線を引く...
-
電気ハンドホールの設置間隔の...
-
円x²+y²=1と直線y=x+mが接する...
-
円を直線で分割すると・・・?
-
直線を含む平面
-
組み合わせの問題
-
座標計算でのTan(θ)-1/Cos(θ)に...
-
不等号をはじめて習うのは?
-
エクセル・パワーポイントなど...
-
グランドにきれいな長方形を描...
-
実数x,yはx^2+y^2=4を満たすと...
-
下の画像の問題(7)なのですが、...
-
直線の傾き「m」の語源
-
120分の番組を1.5倍速で見ると8...
-
なまし鉄線(番線)をまっすぐ...
-
このSを正射影した面積がScosθ...
-
general formとstandard formの...
-
作図の問題です
-
wordの図形の描き方について
おすすめ情報
