線形代数の問題だと思う行列の性質について

n×ｎの正方行列で、
・全ての成分が、1か（－1）
の場合、何か一般的なことが言えるでしょうか？
1と（－1）の配置にパターンはないのですが、
（１）行列式＝０となるための条件
（２）他何か特徴的ななにか
とか言えることがあればいいのですが・・・・。

教えてください。

No.1 ベストアンサー 回答者： stomachman 回答日時： 2025/06/20 09:42

行列式＝０となるための条件　：　おんなじ行、あるいは符号がまるまる逆である以外はおんなじである行が２つ以上ある。

当たり前だけど。

この回答へのお礼

ご指摘ありがとうございます。

お礼日時：2025/06/23 03:37

No.5 回答者： kamiyasiro 回答日時： 2025/06/21 16:33

No.4です。

すみません。n＝5の場合、パターン総数は
2^25＝33554432
ですから、10万回程度では圧倒的に不足ですね。

n＝4までの結果から、法則性のご検討をお願いします。

No.4 回答者： kamiyasiro 回答日時： 2025/06/21 16:23

何か特徴的なことはないか？

例えば、n＝5まで、当該の操作をモンテカルロシミュレーションで各々10万回試行してみました。
そのdet値は、特有のものしか出現せず、各々の回数は次の通りです。

n＝2
___-2_____0_____2
25092_49988_24919

n＝3
___-4_____0_____4
18701_62589_18709

n＝4
__-16____-8_____0_____8____16
__570_16318_66210_16320___581

n＝5
__-48___-32___-16_____0____16____32____48
___67__1841_15438_65447_15297__1814____95

なにか、比率に法則性でもあるのでしょうか。
腕に覚えのある方、宜しくお願いします。

※プログラムのミスで10万ー1回になっていたみたいです。

この回答へのお礼

ありがとうございました。
こういうため仕方もあるんですね。

お礼日時：2025/06/23 03:38

No.3 回答者： mtrajcp 回答日時： 2025/06/21 11:07

2×2の正方行列で、

・全ての成分が,1か(-1)
の場合、
行列式=2,-2,0の3通りしかないから
行列式=(2の倍数)

ある自然数k≧2に対して
k×kの正方行列で、
・全ての成分が,1か(-1)
の場合、
行列式=(2の倍数)
と仮定すると

(k+1)×(k+1)の正方行列で、
・全ての成分が,1か(-1)
の場合、
行列式をk×kの正方行列式の和に余因子展開すれば
行列式=(2の倍数)
となるから

n×nの正方行列で、
・全ての成分が,1か(-1)
の場合、
行列式=(2の倍数)
となる

この回答へのお礼

ありがとうございます。

お礼日時：2025/06/23 03:38

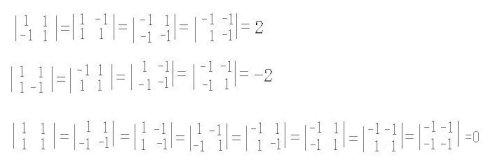
No.2 回答者： kamiyasiro 回答日時： 2025/06/20 14:43

No.1様のおっしゃるように、任意の２列あるいは任意の２行間で、同一配列あるいは逆符号の同一配列があればランクが落ちるのは当然ですね。

あとは、上記の拡張ですが、任意の２列以上の各成分の線形和あるいは２行以上の各成分の線形和が同じ値になる場合（それを線形制約が掛っていると言いますが）、その場合もランクが落ちます。すなわち行列式が０になります。

よって(1)行列式＝０になる条件は「線形制約が掛っている」です。

他の性質については、Tを転置記号とすると、
rank(A)＝rank(ATA)＝rank(AAT)
から導かれる性質でしょうか。

rank(ATA)やrank(AAT)は正方行列ですが、その前のｎ×ｍ行列のＡの段階でランクが落ちていると、ATAやAATもランク落ちします。
ただ、行列の積の結果が１かー1のみになることは、一般的には考えられないですが・・・。

この回答へのお礼

ご指摘ありがとうございます。

お礼日時：2025/06/23 03:37