数学の冬休みの宿題です。
息子は「難しすぎてこんがらがった~!」と投げ出してしまいましたが、私は図を描きながら、なんと条件は整理できたけど、やっぱり????。
どなたかこんなバカ親子に解き方を教えてください。
問題(原文そのまま)
A地点からC地点までの途中にB地点があるジョギングコースがある。A地点からB地点までの上り坂で道のりがxm、B地点からC地点までは下り坂で道のりがymであり、松田さん、竹田さんがこのコースでジョギングした。途中の休憩はないものとする。
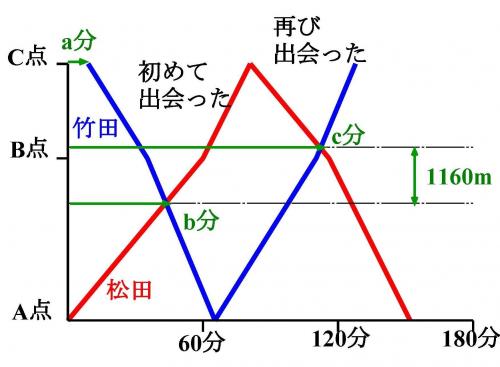
松田さんはA地点をスタートし、C地点で折り返して、再びA地点まで走ってくるのにかかった時間は2時間32分。
A地点からB地点までかかった時間は、B地点からC地点までかかった時間より39分長かった。
松田さんの走る速度は、上り坂は毎分60m、下り坂は毎分100m。
(1)x、yの値をそれぞれ求めなさい。
(2)松田さんが出発してから何分後かに、竹田さんがC地点をスタートし、A地点折り返して、再びC地点まで走たった。するとA地点とB地点の間で二人は初めて出会い、松田さんんがC地点で、竹田さんがC地点でそれぞれ折り返した後、B地点とC地点の間で再び二人は出会った。
最初に出会った地点と再び出会った地点の道のりは1160m。
竹田さんの走る速度は、上り坂は毎分80m、下り坂は毎分120m。
A地点と二人が初めて出会った地点の間の道のりを求めなさい。
A 回答 (8件)
- 最新から表示
- 回答順に表示
No.8
- 回答日時:
みなさんと同じ答えなのですが、1日 何回も計算して、その度に計算間違いがあり、訂正して訂正してやっと同じ答えに辿り着きました
みんな計算が正確ですね!
【僕の解答】
(1)松田さんの走った時間をそのままたして
x / 60 + y / 100 + x / 100 + y / 60 = 152
A から B にかかった時間は B から C より 39分 多かったので
x / 60 = y / 100 + 39
この連立方程式を解くと
x = 3600
y = 2100
(2)松田さんが出発してから竹田さんが出発するまでの時間を a分
松田さんが出発してから竹田さんと初めて出会うまでの時間を b分
松田さんが出発してから竹田さんと再び出会うまでの時間を c分
とします
式を立てる前に、
松田さんの格区間で要した時間は
A→B 3600 / 60 = 60
B → C 2100 / 100 = 21
C → B 2100 / 60 = 35
B → A 3600 / 100 = 36
竹田さんは
C → B 2100 / 80 = 26.65
B → A 3600 / 120 = 30
A → B 3600 / 80 = 45
B → A 2100 / 120 = 17.5 を計算しておきます
初めて出会った時の
松田さんの A からの距離は 60 b
竹田さんの A からの距離は 5700 - 2100 - 120(b - a - 26.25)
= 6750 - 120(b - a)
再び出会った時の
松田さんの A からの距離は 5700 - 60(c - 60 - 21)
= 10560 - 60c
竹田さんの A からの距離は 3600 + 120(c - a - 26.25 - 30 - 45)
= 120(c - a)- 8550
初めて出会った時の距離が等しいとおいて
60 b = 6750 - 120(b - a)
整理すると 6b - 4a = 225
始めた出合った距離より再び出合った距離は 1160m 多いので
60 b + 1160 = 10560 - 60c
整理すると 6b + 6c = 940
(2で割れるけど、後の計算のしやすさを考えてここでとどめた)
再びであった距離が等しいとおいて
10560 - 60c = 120(c - a)- 8550
整理すると 6c - 4a = 637
6b - 4a = 225
6b + 6c = 940
6c - 4a = 637
の連立方程式を解くと
a = 39/4
b = 44
c = 338/3
初めて出合った距離は 60 b = 60 ・ 44 = 2640 メートル
【まとめ】
(1)x = 3600、y = 2100
(2)A地点と二人が初めて出合った地点の間の距離は 2640 メートル
No.7
- 回答日時:
ちょっと解いてみた
No.3,No.4,No.5です。
(2)のほう・・文章そのままに式にしてみる。
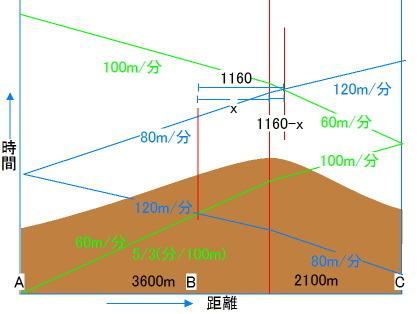
最初に出会った地点と二回目に出会った地点は、(Aから3600mの)坂の頂上の両側にあるので、最初に出会った地点から頂上までの距離をxとする。
松田さん
x/60 + 2100/100 + {2100 - (1160-x)}/60 で出会う
竹田さん
(3600-x)/120 + 3600/80 + (1160-x)/120 で出会う
x/60 + 2100/100 + (940 + x)/60 = (3600 - x)/120 + 3600/80 + (1160 - x)/120
x/60 + 2100/100 + 940/60 + x/60 = 3600/120 - x/120 + 3600/80 + 1160/120 - x/120
x/60 + x/60 + x/120 + x/120 = 3600/120 + 3600/80 + 1160/120 - 2100/100 - 940/60
2x/60 + 2x/120 = 4760/120 - 2100/100 + 3600/80 - 940/60
3x/6 = 4760/12 - 2100/10 + 3600/8 - 940/6
3x = 2380 - 1260 + 2700 - 940
x = 960
よって、3600-x = 2640
No.6
- 回答日時:
(1)x、yの値をそれぞれ求めなさい。
>例えばA地点からB地点までの所要時間をab分(B地点からA地点までの
所要時間をba分)とすると、
ab+bc+cb+ba=152、ab=bc+39、60ab=100ba、100bc=60cb
これらを連立で解くとab=60、bc=21だから
x=60*60=3600(m)=3.6(Km)、y=21*100=2100(m)=2.1(Km)・・・答
(2)は「松田さんがC地点で、竹田さんがA地点でそれぞれ折り返した後」に訂正後、
>松田さんが出発してからx分後かに、竹田さんがC地点をスタートし、
y分後にA地点とB地点の間で二人は初めて出会ったとすると、その間
に松田さんが走った距離は(x+y)*60(m)、竹田さんが走った距離は、C地点
からB地点までの上り2100(m)と、それに要した時間が2100/80=105/4(分)
だからB地点からA地点に向けての下り(y-105/4)*120(m)の合計となり、
A地点とB地点の間の距離が3600mだから、
(x+y)*60+(y-105/4)*120=3600・・・・・(ア)。
再び二人が出会った地点は、初めて出会った地点(A地点からB地点に
向かって(x+y)*60(m)の地点)からの道のりが1160mでB地点とC地点の間
だから、B地点からC地点に向かって(x+y)*60+1160-3600(m)の地点。
初めて出会った地点からその地点まで松田さん走った距離は、A地点から
B地点までの上りの残り3600-(x+y)*60(m)、B地点からC地点までの下り
2100(m)、C地点から再び出会った地点までの上り2100-{(x+y)*60+1160-3600}
=4540-(x+y)*60(m)の合計であり、所要時間は上りが
{3600-(x+y)*60+4540-(x+y)*60}/60=407/3-2(x+y)(分)、下りが2100/100=21(分)
の合計470/3-2(x+y)(分)。
同じく竹田さんが走った距離は、A地点までの下りの残り(x+y)*60(m)、
A地点からB地点までの上り3600(m)、B地点から再び出会った地点までの下り
(x+y)*60+1160-3600=(x+y)*60-2440(m)の合計であり、所要時間は上りが
3600/80=45(分)、下りが{(x+y)*60+(x+y)*60-2440}/120=(x+y)-61/3(分)の合計
(x+y)+74/3(分)。二人の所要時間は等しいから
470/3-2(x+y)=(x+y)+74/3・・・・・(イ)
(ア)と(イ)を連立で解いくと、x=39/4、y=137/4
よって、A地点と二人が初めて出会った地点の間の道のりは
(x+y)*60=(39/4+137/4)*60=2640(m)・・・答
No.3
- 回答日時:
>私は図を描きながら、なんと条件は整理できたけど、やっぱり????。
それで良いです。
確かに複雑な文章題ですね。
まず、文章から時間と距離のグラフを書いてみると良いです。
そして、文章をそのまま式にすることから始めましょう。
単位は分にしておいたほうが良さそうです。
>松田さんはA地点をスタートし、C地点で折り返して、再びA地点まで走ってくるのにかかった時間は2時間32分。
※往路と復路は上下が反転するので・・
A→B x/60
B→C y/100
B←C y/60
A←B x/100
x/60 + y/100 + y/60 + x/100 = 60*2 + 32
(1/60)x + (1/100)y + (1/60)y + (1/100)x = 152
>A地点からB地点までかかった時間は、B地点からC地点までかかった時間より39分長かった。
(1/60)x = (1/100)y + 39
よって、
/ (1/60)x + (1/100)y + (1/60)y + (1/100)x = 152
\ (1/60)x = (1/100)y + 39
が【問1】の連立方程式
/ (1/60)x + (1/100)x + (1/100)y + (1/60)y = 152
\ (1/60)x = (1/100)y + 39
/ (5/300 + 3/300)x + (3/300 + 5/300)y = 152
\ (1/60)x + (-1/100)y = 39
/ (8/300)x + (8/300)y = 152 両辺に300をかける。
\ (1/60)x + (-1/100)y = 39 両辺に300をかける。
/ 8x + 8y = 45600
\ 5x + (-3)y = 11700
/ x + y = 5700
\ 5x + (-3)y = 11700 (1)を3倍して加える
/ x + y = 5700
\ 8x + (0)y = 28800
/ x + y = 5700 (2)を引く
\ x = 3600
/ y = 2100
\ x = 3600
[検算省略]

すみません。(2)は問題文を写し間違っていました。正しくは「松田さんがC地点で、竹田さんがA地点でそれぞれ折り返した後、」です。
(1)の解き方+回答まで丁寧に教えていただきありがとうございました。その後、息子は自力で式はたてる所までできました。式は合っているので、感心してみていると、計算がうまくいかずに、3桁/4桁の分数で答えを出しています。
ありゃ、また英語の単語帳づくりを始めてしまいました。
私は答え合わせができて、すっきりです。(2)にも再チャレンジしてみます。
No.2
- 回答日時:
息子さんにやらせるべきなのでしょうが
なんか懐かしくなったので挑戦してみました。
(1) 往復にかかった時間が2時間32分=152分ということから
x/60 + y/100 + x/100 + y/60 = 152 という式が出せます。
約文通分して整理すると
x+y=5700という式になりますのでこれを(1)とします。
A地点からB地点までかかった時間は、B地点からC地点までかかった時間より39分長かった
ということから
x/60 - y/100 = 39 という式が出せます。
これも約文通分して整理すると
5x - 3y = 11700 となりこれを(2)とします。
あとは(1)と(2)を連立方程式のやりかたで解けば答えが出ます。
(2) やってみましたが分かりませんでした・・・
中一の問題ってこんなに難しかったですっけ・・・?
すみません。(2)は問題文を写し間違っていました。正しくは「松田さんがC地点で、竹田さんがA地点でそれぞれ折り返した後、」です。
(1)を教えていただいた通りにやってみたらできました。息子にはもう少し悩ませてから、教えてどうか考えますね。ありがとうございました。
お探しのQ&Aが見つからない時は、教えて!gooで質問しましょう!
似たような質問が見つかりました
- 地理学 旅人算 3 2022/07/23 09:51
- 地理学 旅人算 2 2022/07/23 11:34
- 地理学 旅人算 1 2022/07/23 01:26
- 数学 この問題を教えて下さいm(_ _)m A地点からB地点を経てC地点まで自転車で行くと15分、歩いて行 5 2022/04/09 22:50
- 数学 この問題の解き方を教えて下さい。 A地点には正確な時計Xがあり、B地点には進み方は正確であるが正しい 2 2022/06/05 22:10
- その他(教育・科学・学問) A地点からB地点までの距離は16mで52秒で到着します。 その間30秒間隔でA地点からは製品が払い出 3 2023/08/19 11:19
- 物理学 時間粒子のクロトンやクローノンを仮想すれば、アキレスは亀を追い越せますよね? 8 2023/07/06 04:20
- ネットワーク 「すれ違う時間」と「すれ違う時間」 3 2023/07/05 14:58
- 数学 LがP地点とQ地点を往復したところ、4時間24分かかった。行きは時速6km、帰りは時速5kmで歩いた 5 2022/06/01 08:35
- 物理学 この問題がわかりません Pは質量m、床の動摩擦係数はμです 画像のようにABC地点のエネルギーを求め 3 2022/09/03 21:36
おすすめ情報
デイリーランキングこのカテゴリの人気デイリーQ&Aランキング
-
ある人が、A地点を出発してから...
-
緊急です!!高校物理の平均の...
-
不等式の文章題
-
距離を求める問題の解き方を教...
-
数学に関する質問です。解き方...
-
違う速度の車「時速の問題」
-
数学の速さの問題について
-
数的処理について教えてください。
-
【数学の問題】箱を1個ずつ運ぶ...
-
ある日の10時20分にA町から甲が...
-
公務員試験 数的処理
-
速度・旅人算の問題です。 ベル...
-
速さの問題
-
道のり・時間・速さについての...
-
甲地から乙地へ向け、A、B、Cの...
-
速度と距離と時間の計算式
-
A.B両地点は20kmある。この地点...
-
中学生の数学です。 答えの求め...
-
この問題の解き方を教えて下さ...
-
中一 一次方程式 解説求む!
マンスリーランキングこのカテゴリの人気マンスリーQ&Aランキング
-
ある人が、A地点を出発してから...
-
なぜ速さは足せないのですか?
-
この問題の解き方を教えて下さ...
-
中学数学です。 家から駅まで、...
-
数学の速さの問題について
-
加重平均距離の計算方法がわか...
-
A地点からB地点を経てC地点に行...
-
行きに35分で歩いた距離を、帰...
-
速さ=距離÷時間について
-
不等式の文章題
-
中1の数学の文字を使った式です
-
甲地から乙地へ向け、A、B、Cの...
-
速さの問題
-
【途中で速さが変わる場合】
-
数学の問題について
-
この問題の解き方を教えて下さ...
-
数学の問題でわからないことが...
-
流水算の問題がわかりません
-
A.B両地点は20kmある。この地点...
-
地点Xと地点Yを結ぶ道路がある...
おすすめ情報
