数学で…

区分求積の問題なんですが…

計算したら負になりました

負になる事ってあり得るんでしょうか？


どなたか教えて下さい

No.4 ベストアンサー 回答者： info22 回答日時： 2009/11/10 11:02

#1です。

A#2で図の色が逆でしたので訂正します。

誤：yの正の領域（赤）と負の領域（青）を差し引きすると青の領域の面積の
正：yの正の領域（青）と負の領域（赤）を差し引きすると赤の領域の面積の

この回答へのお礼

お礼が遅れまして、すいません

何回もわかりやすい解説ありがとうございました
m(__)m

お礼日時：2009/11/10 13:05

No.3 回答者： info22 回答日時： 2009/11/10 10:57

#1です。

A#1の補足の回答

>lim[n→∞] {π/n^2(cos(3π/n)+2cos(6π/n)+…+ncos(3nπ/n)

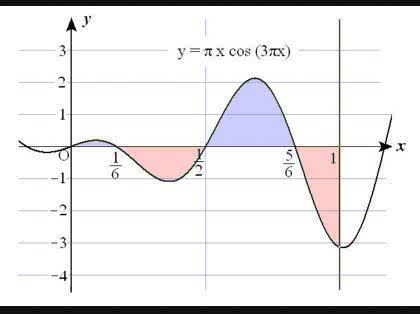
これは　y=πx cos(3πx)　の区間 x=0～1　の定積分になり
　
∫[0→1] πx cos(3πx)dx=-2/(9π)≒-0.07073553

と負になります。

y=πx cos(3πx)　の区間 x=0～1のグラフを添付します。
yの正の領域（赤）と負の領域（青）を差し引きすると青の領域の面積の
方が少し大きいので、積分値が負になることが確認できます。

No.2 回答者： info22 回答日時： 2009/11/09 20:57

#1です。

>計算したら負になりました
>負になる事ってあり得るんでしょうか？
関数の形状や積分範囲のとり方によりますので、
やった計算を補足に書いてください。
チェックします。

（参考）
http://w3e.kanazawa-it.ac.jp/math/category/sekib …

参考URL：http://www.core.kochi-tech.ac.jp/m_inoue/work/pd …

この回答への補足

lim{π/n^2(cos(3π/n)+2cos(6π/n)+…+ncos(3nπ/n)


n→∞です

補足日時：2009/11/09 23:02

No.1 回答者： info22 回答日時： 2009/11/09 17:38

積分

I=∫[a→b] f(x)dx
の積分を求めるとき

x=a～b,f(x)≧0　の場合、
a≦b なら I≧0
a＞b なら I＜0

x=a～b,f(x)≦0　の場合、
a≦b なら I≦0
a＞b なら I＞0

とa,bの積分の方向や被積分関数の符号により
積分値が正になったり負になったりします。
従って。以上のケースの積分値は実際の面積に等しいか、面積に「－符号」が付いた値になったりします。

また、
「積分区間でf(x)の符号が変化する(y=f(x)のグラフがx軸と交わる)場合」
にも、f(x)の正の区間の積分と負の区間の積分が打ち消しあうので、球積面積とは異なり、積分値の符号も正にも、負にもなります。