曲面と点の距離

曲面と点の距離

二葉双曲面の片側(z>0)と点との距離の求め方を教えてください。

例 x^2+y^2-Z^2+1=0 (3/√2,3/√2,-√2)

No.2 ベストアンサー 回答者： info22_ 回答日時： 2010/06/04 06:54

x^2+y^2-z^2+1=0…(1)

xdx+ydy-zdz=0
法線ベクトル：(x,y,-z)
(1)上の点(a,b,c)を通る法線(c>0)の媒介変数表現は
(x,y,z)=(a,b,c)+t(a,b,-c) (c>0)　…(2)
これが点(3/√2,3/√2,-√2)
を通ることから
(3/√2,3/√2,-√2)=(a,b,c)+t(a,b,-c)
∴a= (3/√2)/(1+t), b=(3/√2)/(1+t), c=(√2)/(t-1) …(3)
c>0より　t>1…(4)
(a,b,c)は(1)の点であるから(1)に代入して
{(3/√2)/(1+t)}^2+{(3/√2)/(1+t)}^2-{(√2)/(t-1)}^2+1=0
整理すると
t^4-5t^2-22t+8=0
(t-2)(t^3+2t^2+9t-4)=0
(t-2){(t-1)(t^2+3t+12)+8}=0
(4)より　t>1なので{(t-1)(t^2+3t+12)+8>0
∴t=2
(3)より
　a=b=1/√2,c=√2
点(3/√2,3/√2,-√2)と二葉双曲面の片側(z>0)との距離Lは
は点(3/√2,3/√2,-√2)と点(a,b,c)=(1/√2,1/√2,√2)間の
距離であるから3平方の公式から
　∴L=√(2+2+8)=2√3

図を添付します。

この回答へのお礼

図が添付してあり非常にわかりやすかったです
ありがとうございました

お礼日時：2010/07/11 10:11

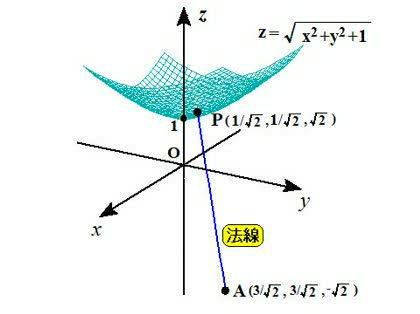
No.3 回答者： aquatarku5 回答日時： 2010/06/04 22:23

NO1の者です。

4次方程式の導出に計算ミスがあったので、訂正します。
NO2の方がすでに名答を用意されていますが、念のため。

（誤）p^2+q^2-r^2+1=t^2(18-4/(2t-1)^2)+1=0
　　　∴72t^4-72t^3+18t^2-4t+1=0　・・・（※）
（正）p^2+q^2-r^2+1=t^2/2・(18-4/(2t-1)^2)+1=0
　　　∴72t^4-72t^3+22t^2-8t+2=0　・・・（※）

（※）は4次方程式で簡単には解き難い感じと思って
いましたが、t=1/3と1/2<t<1の間のtの２つの実数解
を持つようです（No2の方の回答の通り）。前者が求め
る解になっている点は回答NO1の通り。

No.1 回答者： aquatarku5 回答日時： 2010/06/04 06:52

二葉双曲面F(x,y,z)=0の点(x,y,z)における法線ベクトル

=(∂F/∂x, ∂F/∂y, ∂F/∂z)=(2x、2y、-2z)

二葉双曲面上の点(p,q,r)と点(3/√2,3/√2,-√2)
を結ぶベクトルは、上記法線ベクトルと平行であることから、
(p-3/√2):(q-3/√2):(r+√2)=2p:2q:(-2r)
∴この比＝k、1/(1-k)=tとおくと、パラメータtを用いて、
p=3t
q=3t
r=-2t/(2t-1)
を書ける。これを双曲面の式に代入、
p^2+q^2-r^2+1=t^2(18-4/(2t-1)^2)+1=0
∴72t^4-72t^3+18t^2-4t+1=0　・・・（※）
これを解いてt、更に(p,q,r)を求め、点(3/√2,3/√2,-√2)
との距離を求めればよいです。

(※)は、0<t<1/2と、1/2<t<1にそれぞれ解を持ちますが、
片側(z>0)の条件から、前者の方になります。ただこの
4次方程式は簡単には解き難い感じですね。