数学の問題で何度もすみません。下記の問題で困っています。よろしくお願いします。

kは定数とする。方程式|ｘ²-ｘ－２|=2ｘ＋kの異なる実数解の個数を調べよ。

No.3 回答者： stomachman 回答日時： 2015/09/08 05:22

単なる「作業」に過ぎません。

落ち着いて順番にやってきゃ良いんです。「今、何のために何やってるのか」をいつもはっきり自覚して作業を進める。さもないと、式の海で溺れちゃうからね。

(1) 素直に、y=|ｘ²-ｘ－２|のグラフを描く。このためにまず、二次方程式
　　ｘ²-ｘ－２=0
の解（すなわちどこでx軸と交わるか）を計算する。二つの解の中点におけるyの値を計算して、頂点が(1/2, 9/4)であることも分かる。これでおおざっぱなグラフが描けるっしょ。

(2) 描いた曲線と、傾きが2の直線(y=2ｘ＋k)との交点が、問題の方程式の解である。エンピツをその直線の代わりにグラフの上に載せてみて考えれば、何通りの場合に分ける必要があるかはすぐ分かる。kが小さいときには解は0個。kをだんだん大きくして行くと、解の個数は、1個、2個、3個、4個、3個、2個、と変化する、ということがわかるでしょ。これで、一体どういう問題なのか、ということが見えた訳です。

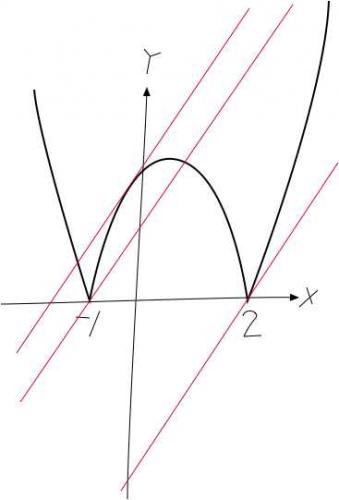
(3) そしたら、「場合分けの丁度境界になるような、傾きが2の直線」を描くのは容易。もちろん3本描くことになる（図の赤い線）。すなわち、
[1] (2,0)を通るもの（このとき、問題の方程式の解は(2,0)だけ）、
[2] (-1,0)を通るもの（このとき、解は(-1,0)のほかにあと2つ）、および
[3] y=-(ｘ²-ｘ－２)に接するもの（このとき、解は接点の他にあと2つ）。

(4) [1][2][3]の切片kを計算する。ちょっとメンドクサイのは[3]の直線で、「二次方程式
　　-(ｘ²-ｘ－２) = 2ｘ＋k
が重解を持つようなkを求む」という問題だと思って解けば[3]の直線のkが決まる。
　あるいはまた、（もし知っていれば）まず微分法を使って「y = -(ｘ²-ｘ－２) の接線の傾きが2になるxは？」を計算し、次に「そのときのyは？」で接点の座標(-1/2, 5/4)を出し、この点を通るようにy=2ｘ＋kの定数kを決める、という手もある。直感的でカンチガイが生じにくいし、それぞれの計算は簡単。

(5) 先に(2)で考えたことによれば、[1],[2],[3]の直線のkの値は[1][2][3]の順に大きくなっているはず。これを確認。あとは(2)で考えた筋書きで答をまとめる。

No.2 回答者： guunagoona2015 回答日時： 2015/09/08 00:39

|ｘ²－ｘ－２|=2ｘ＋k　より

|ｘ²－ｘ－２|－2ｘ＝k ・・・・・(A)
と変形して、
ｙ＝|ｘ²－ｘ－２|－2ｘ ・・・・・（B)　のグラフと　ｙ＝k　のグラフの共有点の個数を調べればよい。

ｘ²－ｘ－２＝(ｘ＋１)(ｘ－２)　だから
(i)　ｘ²－ｘ－２≧０　つまり　ｘ≦－１、　２≦ｘ　のとき
(B)　は
ｙ＝ｘ²－ｘ－２－２ｘ
＝ｘ²－３ｘ－２
＝{ｘ－(３/２)}²－１７/４

(ii)　ｘ²－ｘ－２＜０　つまり　－１＜ｘ＜２　のとき
(B)　は
ｙ＝－ｘ²＋ｘ＋２－２ｘ
＝－ｘ²－ｘ＋２
＝－{ｘ－(１/２)}²＋９/４

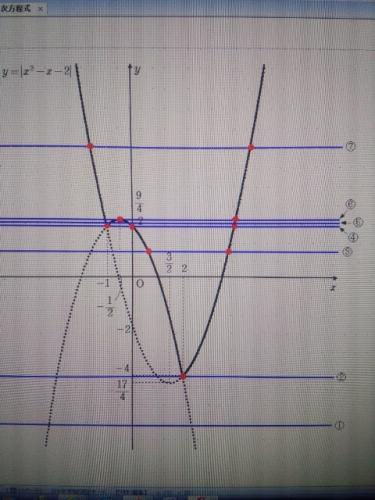
したがって、グラフは添付画像の実線部分

方程式(A)　は、 (B)　のグラフと　ｙ＝k　のグラフの共有点の個数を調べればよいから、
ｋ＜－４　のとき　０ 個
ｋ＝－４　のとき　１ 個
－４＜ｋ＜２、　９/４＜ｋ　のとき　２ 個
ｋ＝２、　９/４　のとき　３ 個
２＜ｋ＜９/４　のとき　４ 個


ｋ＜－４　のとき　０ 個　　　　　　・・・・・①
ｋ＝－４　のとき　１ 個　　　　　　・・・・・②
－４＜ｋ＜２　のとき　２ 個　　　　・・・・・③
ｋ＝２　のとき　３ 個　　　　　　　・・・・・④
２＜ｋ＜９/４　のとき　４ 個 　　　・・・・・⑤　点がうてなかったのですが、共有点が４個あります
９/４　のとき　３ 個 　　　　　　　・・・・・⑥
９/４＜ｋ　のとき　２ 個　 　　　　・・・・・⑦

No.1 回答者： papabeatles 回答日時： 2015/09/07 22:25

|ｘ²-ｘ－２|=2ｘ＋kですので

ｘ²-ｘ－２=2ｘ＋kと
ｘ²-ｘ－２=－2ｘーkの二つの場合を考えることが必要です。
ｘ²-ｘ－２=2ｘ＋kの場合
ｘ＾２－３ｘー（ｋ＋２）＝０
ですので
判別式で
　３＾２＋４（ｋ＋２）を考えます
９＋４ｋ＋８＞０の時に
ｋ＞－１／４のとき解は2つです
９＝－１／４の時重解で解は1つです
９＜－１／４の時解はありません。
ｘ²-ｘ－２=－2ｘ－kの場合
ｘ＾２＋ｘ＋ｋ－２＝０ですので。
判別式で
１－４（ｋ－２）を考えます。
１－４ｋ＋８＝９－４ｋ
９－４ｋ＞０
９／４＞ｋの時解は２つ
９／４＝ｋの時重解で１つ
９／４＜ｋの時解なしです。
即ち
－１／４＜ｋ＜９／４の時解は２つ
K=－１／４、９／４の時解は1つ
ｋ＜－１／４、ｋ＞９／４の時解無しです。