数学 中三 入試問題

はやめにおねがいしたいんですけど...。
(5)お願いします！！

No.7 ベストアンサー 回答者： takoハ 回答日時： 2019/01/18 18:05

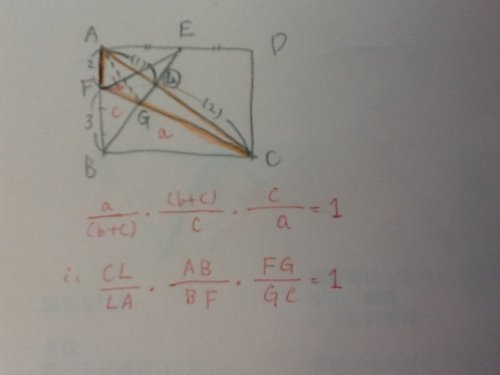
メネラウスの定理とは、相似を利用した面積比から求まる定理！

( △BCG/△ABG)・(△ABG/△BFG)・(△BFG/△BCG) =1

全て相殺されて 1 となる。

第一項は、辺BGを底辺とする2つの三角形で、高さの比が、CL/LAとなる。

第二項は、辺AB:BF=(2+3):3とする三角形で、高さが同じなので、AB/BFとなる。

第三項も、辺FCにおいて、高さが等しい三角形の比が、FG/GCとなる。

これらを、掛けたものがメネラウスの定理である。

また、類似した定理で、チェバの定理もあり、今回も使えるが割愛しました。

尚 高校生なら、ベクトルで解けば、ワンパターンで解けるので参考に後から記載しますね！

この回答へのお礼

ありがとうございます！！

お礼日時：2019/01/18 22:11

No.6 回答者： takoハ 回答日時： 2019/01/18 11:25

座標も可能！

Bを原点として、BCをx軸に、ABをy軸とすれば
A( 0,5),F( 0,3),C( 2,0),E( 1,5)とすれば
直線FCは、y=ー(3/2)・x+3
直線BEは、y=5x
故に、Gの座標は、ー3x /2 +3=5x ∴ x= 6/13 y=5・6/13=30/13 より( 6/13,30/13)
であるから、
FG:GC=6/13 : (2ー6/13)=6:20=3:10 または
=(3ー30/13): 30/13=9:30=3:10

No.5 回答者： takoハ 回答日時： 2019/01/18 10:52

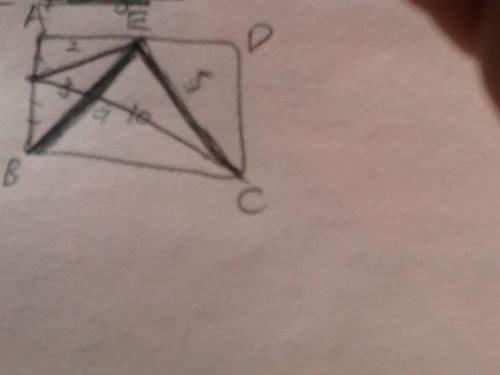
更に、面積でも可能！つまり

AF:BF=2:3より
△AFE=2とすれば、△BFE=3
EとCを結べば、△CED=2+3=5だから △BCE=2+3+5=10
従って、辺FCを底辺とする三角形の比は
高さが点Eからと点Bからの長さが等しいので、そのまま
FGとCGとの比と同じなので、
∴ FG:CG=△BEF:△CBE=3:10

No.4 回答者： takoハ 回答日時： 2019/01/18 10:19

メネラウスの定理でも早いよ！

AとCを結んだ点をLとすれば、△AEL相似△BCLからAE:BC=1:2=AL:CLより
点Bと△ACFにおいて、メネラウスの定理から
CL/LA・AB/BF・FG/GC=2/1・(2+3)/3・FG/GC=1 ∴FG/GC=3/10 ∴FG:GC=3:10

この回答へのお礼

とても参考になりました！
まだメネラウスの定理習ってませんw

お礼日時：2019/01/18 16:49

No.3 回答者： takoハ 回答日時： 2019/01/18 09:54

Fから、CDへの垂線とBEとの交点をJとすれば

△BFJ相似△BAEから、BF:BA=3:(2+3)=3:5=FJ:BEより
また、△FJG相似△BCGから
FG:GC=FJ:2・AE=3:2・5=3:10

補助線を内側にするのも一手！

No.2 回答者： takoハ 回答日時： 2019/01/17 21:03

5)のみ

DAとCFの延長線上の交点をHとする。
∴ △AFH相似△CDHから HA:HD=HF:HC=2:5
また、HF:HC=2:5 ∴ HF:FC=2:(5-2)=2:3=26:39
△EGH相似△BCGから
HE:BC=(2+(5-2)/2 ):(5-2)=3.5:3=7:6=35:30
故に
HF:FG:GC=26: (39-30)または(35-26):30=26:9:30
従って FG:GC=9:30=3:10

No.1 回答者： ココでお困りのワタシ 回答日時： 2019/01/17 20:25

これを見ると分かるでしょうか。

この回答へのお礼

ありがとうございます！！

お礼日時：2019/01/18 16:47