数学Ⅱの領域について x²＋ｙ²≦9、ｘ≧0のとき-ｘ+ｙの最大値最小値を求めよ。 これについてなの

数学Ⅱの領域について

x²＋ｙ²≦9、ｘ≧0のとき-ｘ+ｙの最大値最小値を求めよ。

これについてなのですが、
円の領域が内側でｘ≧0から円の右半分が領域、その時の最大値は(0.3)で3まではわかるのですが最小値が分かりません。
誰か回答お願いします。

No.3 回答者： majimelon37 回答日時： 2019/01/14 03:44

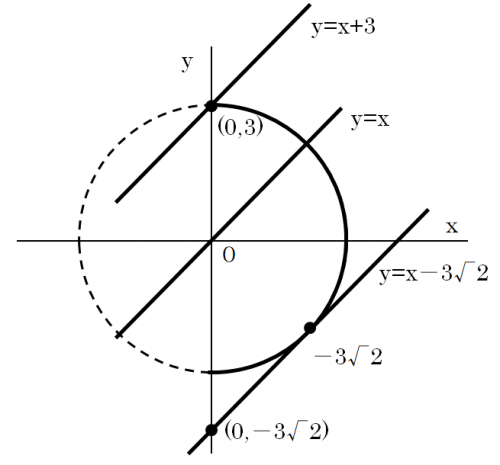
x²＋ｙ²≦9、ｘ≧0　は図の半円である。

-ｘ+ｙ=aとすると、直線ｙ=ｘ+aとなり、図の３本の直線で示される。
a=0のとき原点を通る直線である。上に3だけ移動すると、ｙ=ｘ+3となり、半円の上端(0,3)を通る。
直線を、半円に接するまで下に移動すると、接点は(3/√2,－3/√2)となり、a=3√2となる。これが最小である。
-ｘ+ｙの最大値=3，-ｘ+ｙの最小値=3√2
注意：No.2投稿の（√３/2、ー√3/2）は(3/√2,－3/√2)の書き違いである。

No.2 回答者： kurokurosun 回答日時： 2019/01/13 23:54

-x+y=a　とすると、

y=x+a　ですよね。

これは、傾き１、y切片がaの　直線となります。

x^2+y^2<=9　は、(0,0)を中心とする半径３の円です。

図を描いてみましょう。

円と直線とで交わる時で、aが最大となる時、aが最小となる時。

最小となるのは、（√３/2、ー√3/2）の時ですよね。
この時の、y切片は、a＝-3√2　です。

最大は、逆に、3√2　です。

絵を描けば、暗算でできる問題ですね。

No.1 回答者： varietyknowledge 回答日時： 2019/01/13 22:37

x=Rcosθ, y=Rsinθ（0≦R≦3, 0≦θ＜2π）とすると、x≧0になるためには、cosθ≧0でなければならない。

よって、0≦θ≦π/2または3π/2≦θ＜2π

-x+y
=-Rcosθ+Rsinθ
=√2R(-(1/√2)cosθ+(1/√2)sinθ)
=√2R(sinθcos(π/4)-cosθsin(π/4))
=√2Rsin(θ-(π/4))

θ-(π/4)=π/2のとき最大値√2Rでθ=3π/4となる。
しかし、0≦θ≦π/2であるため、θ=π/2が上限となる。

よって、(π/2)-(π/4)=π/4となり、√2Rsin(π/4)=√2R(1/√2)=R
0≦R≦3より-x+yの最大値は3

θ-(π/4)=3π/2のとき最小値-√2Rでθ=7π/4となる。
これは3π/2≦θ＜2πの範囲にあり、0≦R≦3であるため-x+yの最小値は-3√2になる。

ちなみにx,yは、
x=3*cos(7π/4)=3/√2=(3√2)/2
y=3*sin(7π/4)=-(3/√2)=-(3√2)/2

-x+y=-(3√2)/2 -(3√2)/2=-3√2