確率変数の商の確率分布について

同じ確率変数に従い独立して発生するA,Bの商(A/B)の確率分布を求めたいのですが、やり方が分からず困っています。

確率変数A,Bが互いに独立で、以下の式に従う。
f(x)=15*e^(-x/7.6)　(但し、1<=x<=30)
確率変数U=f(A)/f(B)の確率密度関数はどう求められるのでしょうか？

確率について未熟で記載にわかりにくい部分があると思いますが、宜しくお願い致します。

No.3 回答者： quaestio 回答日時： 2012/02/24 20:45

#1さんの指摘のとおり確率密度分布になっていないのに加えて、A/Bの分布なのかf(A)/f(B)の分布なのかわかりませんね。

どれを求めたいのかはわかりませんが、A/Bの分布を求めてみたので書いておきます。

確率変数A, Bはパラメータλの指数分布の[p, q]の範囲(ただし0 ≦ p < q)を残し切断した分布にiidで従うとします。
パラメータλ(>0)の指数分布の確率密度関数が
Exp(x) = λexp(-λx) (0 ≦ x < ∞)
= 0 (x < 0)
であることから、A, Bの確率密度関数が
f(x) = (λ/(exp(-λp)-exp(-λq)))exp(-λx) (p ≦ x ≦ q)
= 0 (その他)
であることが容易にわかります。

確率変数A, Bを
U = A/B
V = B
と変換すると
dadb = |v|dudv
で、確率密度が0とならない部分は
p/q ≦ u ≦ q/p
p/u ≦ v ≦ q (p/q ≦ u ≦ 1のとき)
p ≦ v ≦ q/u (1 < u ≦ q/pのとき)
であるので、求める確率密度関数は
u < p/qのとき 0
p/q ≦ u ≦ 1のとき
∫_p^{q/p} f(uv)f(v)dv = (1/(exp(-λp)-exp(-λq))^2)(G(λq(u+1))-G(λp(u+1)/u))/(u+1)^2
1 < u ≦ q/pのとき
∫_{p/q}^q f(uv)f(v)dv = (1/(exp(-λp)-exp(-λq))^2)(G(λqt(u+1)/u)-G(λp(u+1)))/(u+1)^2
u > q/pのとき 0
となります。ここでG(x)は形状母数が2で尺度母数が1のガンマ分布の分布関数です。

実際にパラメータを
p = 1
q = 30
λ = 1/7.6
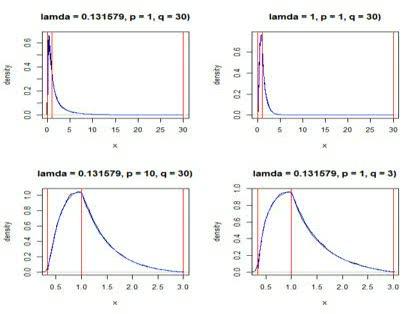
と他３とおり設定して分布を描いてみました。
青い線が理論的な分布、黒い線がシミュレーションによる分布、赤い線は実現値の上限、下限および1を示しています。
シミュレーションはA, Bに従う乱数を10万組発生させて、カーネル密度により分布を描きました。
結果は見てのとおりほとんど一致しました。

グラフの作成は統計解析ソフトR 2.14.0により下記のコードを使いました。
（エラー処理はしてません）

# 理論的な確率密度関数
myPdf <- function(x, lamda, p, q)
{
results <- numeric(length(x))

tmp <- 1 / (exp(-lamda * p) - exp(-lamda * q))^2
flag <- x >= p / q & x <= 1
results [flag] <- tmp * (pgamma(lamda * q * (x[flag] + 1), 2) - pgamma(lamda * p * (x[flag] + 1) / x[flag], 2)) / (x[flag] + 1)^2
flag <- x > 1 & x <= q / p
results [flag] <- tmp * (pgamma(lamda * q * (x[flag] + 1) / x[flag], 2) - pgamma(lamda * p * (x[flag] + 1), 2)) / (x[flag] + 1)^2

return(results)
}

# 乱数の発生
myRnd <- function(n, lamda, p, q)
{
results <- numeric(n)

i = 0
while (i < n) {
tmp <- rexp(2, lamda)
if (sum(tmp >= p & tmp <= q) == 2) {
i <- i + 1
results[i] <- tmp[1] / tmp[2]
}
}

return(results)
}

# シミュレーションの実施と分布の描画
sim <- function(n = 100000, lamda, p, q)
{
title <- sprintf("lamda = %g, p = %g, q = %g)", lamda, p, q)
x <- myRnd(n, lamda, p, q)

plot(density(x), xlim = c(p / q, q / p), main = "", xlab = "", ylab = "", xaxt = "n", yaxt = "n")
par(new = T)
plot(function(x) myPdf(x, lamda, p, q), xlim = c(p / q, q / p), ylab = "density", col = "blue", main= title)

abline(v = p / q, col = "red")
abline(v = 1, col = "red")
abline(v = q / p, col = "red")
}

par(mfrow = c(2, 2))
sim(100000, 1 / 7.6, 1, 30)
sim(100000, 1, 1, 30)
sim(100000, 1 / 7.6, 10, 30)
sim(100000, 1 / 7.6, 1, 3)
par(mfrow = c(1, 1))

No.2 回答者： drmuraberg 回答日時： 2012/02/20 12:28

和と積の確率密度は聞くけど、商は？？と言う程度の者です。

興味が合って検索したら下のHPが見つかりました。
http://wkouw.web.fc2.com/MYPEDIA_math/Word_sekin …

商の確率密度の式の積分を和に置換えて数値計算できるのではないでしょうか。
nも30と少なく、幸いXもYもゼロでは無いのでX/Yも無限大には成らないし。

昔三重積分（和）をベーシックで計算した経験から、マクロで計算できるとは
思いますが。残念ながらマクロは不案内です。

確率密度ですから、104.605で割ってΣf(x)=1と成るように規格化して置いた方が
無難です。

この回答へのお礼

なるほど・・・。
用途を考えるとシミュレーション代用できそうなのでやって見ることとします。

ありがとう御座います

お礼日時：2012/02/20 14:18

No.1 回答者： d_p 回答日時： 2012/02/19 21:42

f が確率分布になってない