抵抗値計算

三角形の左辺から時計回りに、R1,R2,R3とデルタ接続された回路において、各頂点間の抵抗値を測り、その結果から、R1,R2,R3を算出する計算式を教えてください。

No.4 ベストアンサー 回答者： noname#154783 回答日時： 2011/03/15 12:21

きっと私の結果(ANo.1)とANo.3さんの結果は同じなんでしょう（確認してませんけど(苦笑)）．

> 質問内容はこの通りなのですが・・・ここから先が問題です。(-_-;)

「ここから先」というのは... ひょっとしてご質問の「R1,R2,R3を算出する計算式」っていうのは計算結果だけじゃなく，その導出過程も必要ということでしょうか．

ANo.1の導出過程は

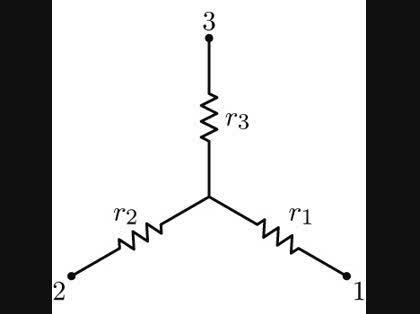
まず，問題のΔ結線(ANo.1の図)を今回の添付図のY結線にΔ→Y変換します：
r1 = R2 R3/(R1+R2+R3),
r2 = R3 R1/(R1+R2+R3),
r3 = R2 R2/(R1+R2+R3).

そうすると，2端子間の抵抗値は次のように表されます：
R31 = r3 + r1,
R12 = r1 + r2,
R23 = r2 + r3.

これをr1,r2,r3について解くと，
r1 = (1/2)(R31+R12-R23),
r2 = (1/2)(R12+R23-R31),
r3 = (1/2)(R23+R31-R12).

Y→Δ変換で元に戻して
R1 = (r2r3+r3r1+r1r2)/r1,
R2 = (r2r3+r3r1+r1r2)/r2,
R3 = (r2r3+r3r1+r1r2)/r3.

これらの式の分子はすべて同じで，
r2r3+r3r1+r1r2
= (1/4)×
{ (R23^2-R31^2-R12^2+2R31R12)
+ (R23^2-R31^2-R12^2+2R31R12)
+ (R23^2-R31^2-R12^2+2R31R12) }
= (1/4){-R23^2-R31^2-R12^2+2(R23R31+R31R12+R12R23)}.

したがって，
R1
= (r2r3+r3r1+r1r2)/r1
= (1/4){-R23^2-R31^2-R12^2+2(R23R31+R31R12+R12R23)}/{(1/2)(R31+R12-R23)}
= (1/2){R23^2+R31^2+R12^2-2(R23R31+R31R12+R12R23)}/(R23-R31-R12).

R2,R3に対しても同様にしてANo.1の解が得られます．

検算します．
ANo.2の補足の場合，
R23 = 338.5Ω，R31 = 615.4Ω，R12 = 461.5Ω
に対して，

(1/2){R23^2+R31^2+R12^2-2(R23R31+R31R12+R12R23)}
= -295396.92

R23-R31-R12 = -738.4

∴R1 = 295396.92/738.4 = 400.05 [Ω].

R2, R3も同様です．

ただ，ANo.1のままだと，分母も分子もマイナスになってしまうので，次のように書き直しておいたほうがよいのでしょう：
R1 = {(R31R12+R12R23+R23R31)-(1/2)(R23^2+R31^2+R12^2)}/(R31+R12-R23),
R2 = {(R31R12+R12R23+R23R31)-(1/2)(R23^2+R31^2+R12^2)}/(R12+R23-R31),
R3 = {(R31R12+R12R23+R23R31)-(1/2)(R23^2+R31^2+R12^2)}/(R23+R31-R12).

相変わらずいかめしい式ですが，R1,R2,R3とも分子は共通で，なおかつ，R23,R31,R31の対称式になっています．

これで，原理的にはΔ結線の2端子間の抵抗R23,R31,R12をテスタかなんかで実測し，上の式で計算すればR1,R2,R3が得られるはず．

この回答への補足

Δ→Y変換は一番初めに閃いて、「電気の教科書を開いてみようかなー」と思っていたのですが、解に結びつける自信がありませんでした。
Δ→Y変換はこのような使い方をするのですね。
（T結線の場合は簡単に求まるので、何とかつなげられないかと悩んでいました）

丁寧なご回答有難うございました。

補足日時：2011/03/15 13:50

この回答へのお礼

重ねてのご回答誠に有難うございました。

お礼日時：2011/03/15 15:32

No.3 回答者： Executione 回答日時： 2011/03/15 08:13

＃２です。

大変失礼しました。

＞□=2・(R1R2+R2R3+R1R3)/△　・・・1式

＞x=□-2R23
＞y=□-2R31
＞z=□-2R12

この部分は、良く見ると2倍されていました。
次のように訂正します。

2x=□-2R23
2y=□-2R31
2z=□-2R12

x,y,zが2倍されたまま計算していきますと、5,6,7式は2が約分され、右辺は2倍が消えますが、左辺は2倍が残り、最終的に

R1=(xy+yz+zx)/(2x)
R2=(xy+yz+zx)/(2y)
R3=(xy+yz+zx)/(2z)

となります。

この回答への補足

ご回答くださいまして有難うございました。
大変役に立ちました。
ポイントのほうは申し訳ないですが、先着順ということにさせていただきます。
済みませんでした。

補足日時：2011/03/15 15:31

この回答へのお礼

早速のご訂正有難うございました。
大変助かりました。

お礼日時：2011/03/15 13:36

No.2 回答者： Executione 回答日時： 2011/03/14 11:26

＃１さんの図を借ります。

R23=R1(R2+R3)/(R1+R2+R3)
R31=R2(R1+R3)/(R1+R2+R3)
R12=R3(R1+R2)/(R1+R2+R3)

□=R12+R23+R31　とおく。
△=R1+R2+R3　とおく。

□=2・(R1R2+R2R3+R1R3)/△　・・・1式

x=□-2R23
y=□-2R31
z=□-2R12

とおく。
R12、R23、R31は、測定値なので、x,y,zは定数になるので、あらかじめ計算しておくと計算

が簡単になります。

x=□-2R23=R2R3/△　・・・2式
y=□-2R31=R1R3/△　・・・3式
z=□-2R12=R1R2/△　・・・4式

ここで、2,3,4式より
x/y=(R2/R1)　・・・5式
y/z=(R3/R2)　・・・6式
z/x=(R1/R3)　・・・7式

5,6,7式より
R1=(y/x)R2　・・・8式
R2=(z/y)R3　・・・9式
R3=(x/z)R1　・・・10式

9,10式を2式の右辺に代入。・・・★
x={(z/y)R3・(x/z)R1}/△
　={(x/y)R1R3}/△

△を次のように変形する。
△=R1+R2+R3
　=R1{1+(R2/R1)+(R3/R1)}

したがって、
x={(x/y)R1R3}/R1{1+(R2/R1)+(R3/R1)}　
={(x/y)R3}/{1+(R2/R1)+(R3/R1)}　・・・11式

11式の分子R3に10式を代入。
11式の分母に5式および7式の逆数を代入。

x={(x/y)・(x/z)R1}/{1+(x/y)+(x/z)}
={(x^2・R1)/(yz)}/{1+(x/y)+(x/z)}
=(x^2・R1)/(xy+yz+zx)

ゆえに、
R1=(xy+yz+zx)/x
x,y,zは定数なので、求めることが出来ます。

同様に、★に戻ってR2、R3を求めます。
計算はしてませんが、多分、
R2=(xy+yz+zx)/y
R3=(xy+yz+zx)/z

この回答への補足

すみません。
どこかおかしいです。

[例]
R1=400, R2=1600, R3=600　とすると、
R23=338.5, R31=615.4, R12=461.5, □=1415.4となり、
x=738.4, y=184.6, z=492.4　となるので、これから計算したR1,R2,R3は
上記の値のちょうど２倍になります。

どこで間違ったのでしょう？

補足日時：2011/03/15 00:16

この回答へのお礼

すばらしい計算力です。
こういう頭脳はどうして培われたのでしょう？
教えてください。

お礼日時：2011/03/15 00:18

No.1 回答者： noname#154783 回答日時： 2011/03/14 07:29

決してこの分野の専門家じゃないので黙っていようかとも思いましたが，レスもついてないみたいですし，書いてみました．

> 三角形の左辺

というのがよくわからなかったのですが，とりあえず添付した図のような状況であると解釈し，図のように，端子に名前を付けました．

で，例えば，端子2と端子3の間の抵抗値をR23などと名前を付けると，

R1 = (1/2){(R23^2+R31^2+R12^2)-2(R31R12+R12R23+R23R31)}/{R23-(R31+R12)},
R2 = (1/2){(R23^2+R31^2+R12^2)-2(R31R12+R12R23+R23R31)}/{R31-(R12+R23)},
R3 = (1/2){(R23^2+R31^2+R12^2)-2(R31R12+R12R23+R23R31)}/{R12-(R23+R31)}

という式が得られますので，これでどうにかならんでしょうか．

この回答への補足

質問内容はこの通りなのですが・・・ここから先が問題です。(-_-;)

補足日時：2011/03/14 22:35