力学の問題（ドラム）

Question

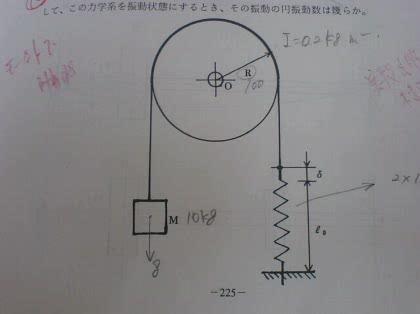
機械力学の問題で添付のドラムの問題ですが、固有振動数をエネルギー保存で解きたいのですが、答えを導き出せません。

1/2mv^2+1/2Iw^2=1/2kx^2
（m：ワーク質量　v:速度　I:ドラム慣性モーメント　w:ドラム角速度　k:バネ定数　x:バネたわみ）

で解きはじめました。

v=rwより（rドラム半径）

1/2m*r^2*w^2+1/2Iw^2=1/2kx^2

まとめると
m*r^2*w^2+Iw^2=kx^2

w^2(mr^2+I)=kx^2

w=√(kx^2/mr^2+I)

ここでｘ＾2を置き換えたいのですが、よく分からなくなってしまいます。

ｋｘ＾2＝k*rθ*rで
mv^2+Iw^2=kx^2というモーメントで計算してある答えも類似問題で見つけたのですが
それですとk*rθ*rでしたらトルク値になりますから式自体は理解できるのですが

w=√(kx^2/mr^2+I)からｘ＾2を置き換えたいとなると
xはたわみですからrθですよね。となるとx^2=r^2*θ^2で

θ＾2って何なんですか？

なんだかよく分かりません。

説明が上手に出来ず、質問が下手ですが、そもそもエネルギー保存で解けるのですか？

ほんと説明が下手で申し訳ありません。

rnakamra · Accepted Answer

まず、エネルギー保存の式が違う。

(1/2)mv^2-mgx+(1/2)Iw^2+(1/2)kx^2=一定

これが正しいエネルギー保存の式。位置エネルギーの項はxの原点を平衡の位置にずらすことで消すことが可能。
質問者の式はバネの弾性エネルギーが右辺にあるがこれは明らかに間違い。

w=v/r
ですのでこの式は
(1/2)(m+I/r^2)v^2+(1/2)kx^2=一定
と書き直すことができるが、これはバネ定数kのバネに質量m+I/r^2の質点をつけた場合の単振動の式と同じと考えればよいでしょう。

yokkun831 · Answer

>θ＾2って何なんですか？

xは何でしょうか？　xは初期変位です。したがって，θは円筒の初期角変位ですね？

でも，初めのエネルギーと終わりのエネルギーを比較するのではなく，一般の変位x におけるエネルギーを計算すればよいのです。xをつり合い位置からの変位として，

E = 1/2・mr^2ω^2 + 1/2・Iω^2 + 1/2・kx^2
=  1/2・(mr^2+I)ω^2 + 1/2・kr^2θ^2

単振動のエネルギー保存

E = 1/2・MV^2 + 1/2・KX^2

と比較して，
M → mr^2 + I
V=dX/dt → ω=dθ/dt
K → kr^2
X → θ

固有角振動数は，

Ω = √(K/M) = √{ kr^2/(mr^2+I) }

となると思います。

まず、エネルギー保存の式が違う。