2013/12/30 に質問があり、その日に回答、
ベストアンサーを貰ってしまったのですが、
僕にもわからず悩んでいた所があり、
再質問します
問題文:
図のように、平行四辺形の各辺の3等分点の一つと頂点を結んだ線を
引きます。網目部分の面積は平行四辺形の面積の何倍ですか。
答えは: 2/5倍
まず、僕の回答は面積の問題を解く上で、
平行四辺形を高さを変えず、長方形にしても
面積は変わらない
長方形を正方形に変形しても、面積の比は
変わらない
として問題を解き、その方針は、簡単に
速く解答する手段として、悪くないと思います
ただ、平行四辺形のまま解答するとすると、
どんな解答がスマートか知りたいです
僕が考えた平行四辺形のままの解答は:
△ ABH、△BCE、△CDF、△ADG いずれの面積も
大きな平行四辺形の面積 S の
1/2 × 1/3 = 1/6 であること
a + b + c = 1/6 S
a + c + d = 1/6 S
△ABS と △EBP、△BCP と △FCQ の面積の比が
9:1 であること
b + c = 9c → b = 8c
a + d = 9a → d = 8a
上記を解くと
a + c = 1/30 S
b + d = 8/30 S
a + b + c + d = 3/10 S
編み目部分の四角形の面積は
S - 2 × 3/10 S = 2/5 S
と一応、正解は得られたのですが、
本当は a = c、b = d だと思うのに、
証明できず、a + c、b + d で計算して
面倒臭かったことです
a = c、b = d をどう証明するのか
および
もっとスマートな解答をお願いします

No.4ベストアンサー
- 回答日時:
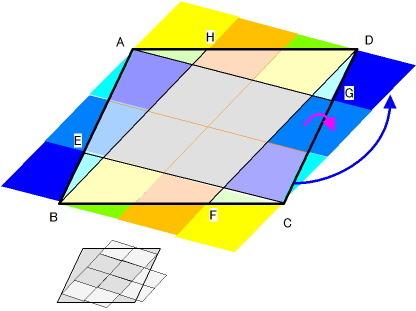
小学生なので、相似は使わずに・・
詳しい説明は省きますが・・
この回答への補足
僕の疑問に真っ正面から正解をくださった No.1 さん、
大きな平行四辺形と小さな平行四辺形の間にもう1つ
平行四辺形があり、それに着目すると「スマート」に
解けることを教えてくださった No.3さん、
まさに「目から鱗」の No.4 さん、
小学生に1番 教えやすいかもという親しみの持てる
回答の No.7 さん、
どれも僕にとってはベストアンサーの二乗の価値があり、
どれもベストアンサーにしたかったのですが、
1番 インパクトの強い図の No.4 をベストアンサーに
選ばせて頂きました
みなさん、本当にありがとうございます
最初、図を見た時は「ルービックキューブ?!」と
恐れおののきましたが、
感動的にすごいわかりやすいです
本当にまったく説明いりませんね \(*^O^*)/
No.8
- 回答日時:
せめて、元の問題が何かをきちんと示しておかないと・・・
#4さんのとおりに、基準とする小さい平行四辺形を網目部分に対するものとしてあげれば、
もとの平行四辺形は 10個分、網目部分は 4個分と出せます。
高校数学以上に手を出すと、
どうしても相似とかは当たり前のものとして使ってしまいがちだが、
小学生なら三角形の面積比が高さの比や底辺の比ぐらいでしか考えられないことを考慮すべき。
参考URL:http://oshiete.goo.ne.jp/qa/8406300.html
No.7
- 回答日時:
算数的(?)に解くならば、図形の一部(三角形AED)を切って、平行四辺形の下に移動させる方法がわかりやすいと思います。
もとの平行四辺形の各辺の三等分した点をずらして結べば、小さな平行四辺形が10個分できます。求める網目の平行四辺形はこの小さな平行四辺形4個でできていますので、面積比は 4/10=2/5 です。
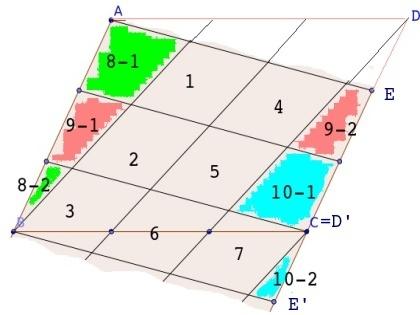
No.4 さんの図を見て、
僕は網目の平行四辺形の4分の1を1つと数えましたが、
No.7 さんの解答も数え方同じで わかりやすいです
小学生とか、こっちの方を思いつく子が多いかもしれません
No.6
- 回答日時:
平行四辺形の面積は「平方網目 g^2」で表せそう。
以下、今まで出てきたシナリオをまとめるだけですが…。
まず、最小三角形の面積 s は、網目部分を囲んでいる 4 つの合同三角形 1 個中に 9 (=1+3+5) 個分ある。
また、各合同三角形に含まれている 2 つの最小三角形は同面積。← これが「鍵命題」
したがって、10*s = 3/2 (g^2) 。
合同三角形 1 個の面積 t = (3/2)*(9/10) = (g^2) 。
平行四辺形全体の面積は 9 (g^2)。
以上から、網目部分面積は、
9 - 4*(3/2)*(9/10) = 9 - 3*9/5 = 9*2/5
らしい。
残念ながら、この説明は児童に通じないでしょうネ。
>まず、最小三角形の面積 s は、網目部分を囲んでいる 4 >つの合同三角形 1 個中に 9 (=1+3+5) 個分ある。
>また、各合同三角形に含まれている 2 つの最小三角形は同>面積。← これが「鍵命題」
そこまでは理解できました
>したがって、10*s = 3/2 (g^2) 。
ここで頭、ついて行けなくなりました
後でゆっくりじっくり考えてみます
No.3
- 回答日時:
スマートな回答ではないのかもしれませんが…
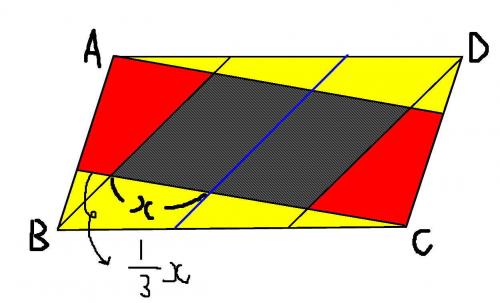
まず,図のように黄色の三角形は全体の1/6なので,引き算します。
そうすると残りは全体の2/3
残りの図形は平行四辺形になるので,網掛けの図形との比はそのまま底辺の比になります。
2X:3X+1/3X=2:10/3 簡単にすると6:10 さらに3:5
網掛けの図形は残りの図形の3/5になります。
最初に戻ると,全体の2/3でさらに3/5なので 2/3*3/5
よって2/5倍
いかがでしょうか?
どっちにしても小学生にできるのかな?
No.1
- 回答日時:
まあ相似関係は使わないといけないでしょうが...
例えば平行四辺形ABCDの各頂点、及び各辺の上にある3等分点をAから反時計回りに
順にA,J,K,B,L,M,C,N,O,D,P,Q,(Aに戻る)として、
今BQとAOとの交点をR、BQとJOとの交点をSとすると、ADとJOとは明らかに平行で、
AQ:JS=AB:JB=3:2, 従ってJS:SO=2:(9-2) = 2:7でAD=JOだから
QR:RS=AQ:SO=3:7
BS:SQ=BJ:JA=2:1 = 20:10よりBS:SR:RQ=20:7:3,
三角形AQR = (3/30)三角形AQB = (1/6) * (1/10)平行四辺形ABCDで、あと3つの
「小さい3角形」も等しく(1/6) * (1/10)平行四辺形ABCDであることは明らかです。
No.1 の解答ありがとうございます
質問した時に画像も用意し、添付したつもりだったのですが
添付しそこねており、ごめんなさい
補助線 JO を引くことで、順繰りに各線の長さの比が
わかるのですね!
スッキリしました
お探しのQ&Aが見つからない時は、教えて!gooで質問しましょう!
おすすめ情報
デイリーランキングこのカテゴリの人気デイリーQ&Aランキング
-
身近にある平行四辺形
-
中2数学の「平行四辺形の2組の...
-
ACを1:2に分ける点pの作図
-
数1
-
次の正四面体のA-C,A-D,B-Cの中...
-
数学 問題
-
円に内接する等脚台形について。
-
「美女と野獣」のベル役だった...
-
キログラム(kg)を立米(m3)...
-
1トンは何リットルでしょう。
-
2㎡って何センチですか?
-
40%に縮小したものを100%に戻...
-
大至急お願いします! 凄くくだ...
-
円弧とはどんな形ですか? 画像...
-
大至急お願いします!椎茸切っ...
-
体積を重さに置き換えるには?
-
南都銀行のキャッシュカードの...
-
オベリスク体積算定式の導出法
-
0.1ccってどのくらいの量ですか...
-
円錐の展開図面を描きたい
マンスリーランキングこのカテゴリの人気マンスリーQ&Aランキング
おすすめ情報
