変換変換と極座標変換の面積 微積問題

微積に関する問題です。

【問題】
関数 u=x^2-xy+y^2 , v=x^2+xy+y^2 によって定められる(x,y)平面から(u,v)平面への写像Fを考える。(x,y)平面の円の内部 D:x^2+(y-1)^2≦1/2 のFによる像ε=F(D)の面積を求めよ。

No.5 回答者： info222_ 回答日時： 2014/09/05 18:03

>私は求める面積というのを間違っていたと思いました。

>単に変数変換して、極座標変換するのではなく写像Fがどういうものか、そしてそれがどのように表してあるのかを考える必要があったと思います。

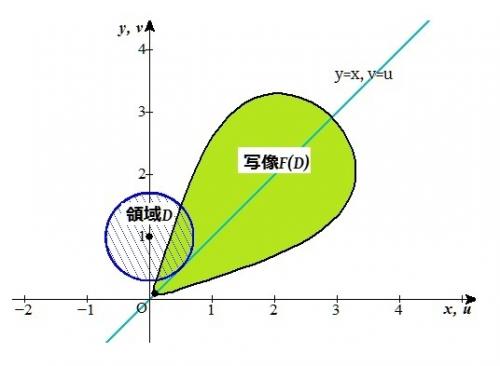
写像F(D)によって, (u,v)の領域は添付図の曲線の内部（周を含む）ようになります。
この領域の周の境界線の方程式はアフィン変換を使って求めることができます。


>ヤコビアンを使った重積分変換は
この場合、行列式を求めると同様に行います。
>もしかしたらヤコビアンには絶対値がつくのですか？

そう、絶対値がつきます。

>∂(u,v)/∂(x,y)=4(x^2-y^2)によってヤコビアンを求め、
>xyに関してDの領域で面積を求めるという考えにいきつきました。
>∮∮D 4(x^2-y^2)dxdy

　面積S=∬[F(D)] dudv = ∬[D] |J|dxdy　…（※1）

>となりました。

この記号「∮」は周回積分または閉ループに沿っての積分の記号ですから、普通の積分では使っていけません。「∫」、「∬」などを使ってください。

|J|=|4(x^2-y^2)|

■■領域Dの「x^2+(y-1)^2≦1/2」は添付図のy=xの直線の上部にあるので「y≧x」となります。■■

■■したがって　|J|=4(y^2-x^2)　■■
となります。

（※1）より

S=∬[D] 4(y^2-x^2) dxdy　…(※2)

このままでも積分できますが、

>そこで、極座標変換を x=rcosθ,y=1+rsinθと置いたのですが、
>どうしても答えがマイナスになってしまいます。

たぶん

　 S=∬[D] J dxdy= ∬[D} 4(x^2-y^2) dxdy
　
で計算されたため積分値がマイナスになったのでしょう。

（※2）を計算すれば正しい結果が得られます。

　 S=∬[D] J dxdy= ∬[D} 4(ｙ^2-x^2) dxdy
　　=4∫[r:0,1/√2] dr ∫[θ:-π/2, 3π/2] {(1+rsinθ)^2-r^2*(cosθ)^2} dr
　　=2π

No.4 回答者： Tacosan 回答日時： 2014/09/05 16:43

もちろんヤコビアンには絶対値が必要です. この問題だと積分領域 D 全域で y^2 ≧ x^2 なので被積分関数は 4(x^2-y^2) ではなく |4(x^2-y^2)| = 4(y^2-x^2) となります.

あと, F が 1対1 であることは確認しておく必要がありますね. F が 1対1 なら F(D) 上の積分を D 上の積分に単純に置き換えることができますが, 1対1 じゃないと変な部分を重複して計算しちゃうことになりますんで (これは 1変数でも同じことです: 1変数の変数変換では「1対1」と「狭義単調」が同じ意味になりますが).

No.3 回答者： Tacosan 回答日時： 2014/09/05 15:44

そう, ヤコビアンを使って変形するのが (基本的には) 正しい. とはいってもまだまだ突っ込むところはあります.

まず, 本当にそのように変換していいというのはどのように確認しましたか? 変数変換において「任意の写像を使っていい」わけではないということは理解していますか?

また, ヤコビアンを使った重積分の変換を, もう一度確認してください. 実はほんのちょっと間違っています (「答えがマイナスになってしまいます」の原因はここ).

この回答へのお礼

何度もありがとうございます。

私は求める面積というのを間違っていたと思いました。
単に変数変換して、極座標変換するのではなく写像Fがどういうものか、そしてそれがどのように表してあるのかを考える必要があったと思います。

ヤコビアンを使った重積分変換は
この場合、行列式を求めると同様に行います。
もしかしたらヤコビアンには絶対値がつくのですか？

何度も本当にありがとうございます。
ご指摘お願いします！

お礼日時：2014/09/05 16:06

No.2 回答者： Tacosan 回答日時： 2014/09/05 14:10

「変数変換した後にDの領域をうまく求めれないです」の意味がよくわからんです. 「変数変換した後」の「D の領域」って, どういうことですか? ひょっとして F(D) のことでしょうか? もしそうだとしたら, その形がここではあまり意味を持たないといっておきましょう.

そんなことより大事なことがあるんです.

この回答へのお礼

ありがとうございます！
結局は、∂(u,v)/∂(x,y)=4(x^2-y^2)によってヤコビアンを求め、
xyに関してDの領域で面積を求めるという考えにいきつきました。
∮∮D 4(x^2-y^2)dxdy
となりました。
そこで、極座標変換を x=rcosθ,y=1+rsinθと置いたのですが、どうしてもこたえが答えがマイナスになってしまいます。
どこかおかしいとこでもありますか？
お願いします！

お礼日時：2014/09/05 14:57

No.1 回答者： Tacosan 回答日時： 2014/09/05 12:15

で質問はなんですか? まさか「自分で考える気はないのでそのまま暗記できるように全てを教えてほしい」などとは言いませんよね?

この回答への補足

変数変換して、極座標変換することは分かっているのですが、
変数変換した後にDの領域をうまく求めれないです。
そこがいまは1番難しいと思っています。
説明不足ですみません。

補足日時：2014/09/05 12:32