三角関数について。

次の問題がわかりません。教えていただけると幸いです。53,54,55,56です。

質問者からの補足コメント

• 

  53,54,56を詳しく教えていただきたいのです。教えていただけると幸いです。

  No.1の回答に寄せられた補足コメントです。 補足日時：2019/04/01 08:46

No.4 回答者： takoハ 回答日時： 2019/03/29 21:49

追記 △ABC相似△AFEから比の関係の方が早い！

または、座標軸変換より
https://oshiete.goo.ne.jp/qa/11013825.html
から、
cosθ=3/√10 ,sinθ=1/√10 から、B(3,0)は、
X=xcosθ+ysinθ=3x/√10 +y/√10 ……(1)
Y=ーxsinθ+ycosθ=ーx/√10 +ycosθ=ーx/√10 +3y/√10 ………(2)
ここで、b
B(3,0)を代入すれば、X=9/√10 , Y=ー3/√10
Y=0(新しいX軸)に対しての対称点Dは、(9/√10 ,3/√１０ )であるから、
9/√10=3x/√10 +y/√10 ……(1)'
3/√10=ーx/√10 +3y/√10 ……(2)'
∴ 3x+y=9 ,ーx+3y=3 からx=12/5 ,y=9/5
故に、a=(9/5)/(12/5)=9/12=3/4

No.3 回答者： takoハ 回答日時： 2019/03/29 21:05

55だけ！y=x/3 とy=0(x軸)とのなす角度をθとすれば、tanθ=1/3より

a=tan2θ=2tanθ/(1ーtan^2θ)=2・(1/3)/(1ー(1/3)^2))=(2/3)/(8/9)=3/4

または、点と距離の公式から
y=x/3 上の点(3,1)から、y=axまでの距離が1になればいいので
I a・3ー1 I/√(a^2 +(-1)^2 )
平方して
(3aー1)^2=a^2 +1 ∴ 9a^2ー6a+1=a^2+1 ∴8a^2ー6a=2a(4aー3)=0より
a=0はx軸で不適なので、a=3/4

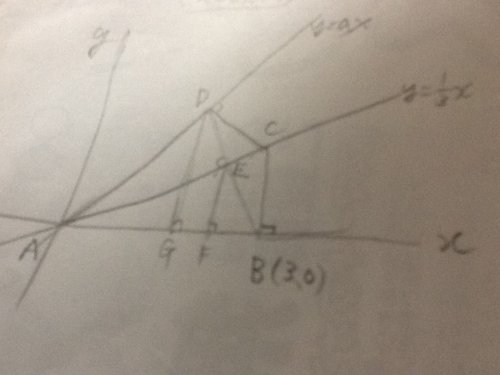
初等幾何でも解ける！図より
AB=AD=3 ,BC=CD=1 三平方の定理より
AC=√(3^2+1^2)=√10
∠ BEC=∠ ABC=∠ ADC=90°より
△ABCの面積=(1/2)・3・1=(1/2)・AC・BE =(1/2)√10・BE ∴ BE=3/√10
△BECは直角三角形より、三平方の定理より
CE=√ (1^2ー(3/√10)^2 )=1/√10
∴AE=√10ーCE=9/√10
△AEF相似△ABCより
AE:AC=EF:BC ∴ 9/√10 : √10=EF: BC=EF:1 ∴ EF=9/10
△BEF相似△BDG かつBE=DEより中点連結定理から
DG=2・EF=2・9/10=9/5
また、△ADGにおいて、三平方の定理より
AG=√(3^2ー(9/5)^2 )=12/5
よって、
a=DG/AG=(9/5)/(12/5)=9/12=3/4

No.2 回答者： takoハ 回答日時： 2019/03/29 20:26

55だけ！y=x/3 とy=0(x軸)とのなす角度をθとすれば、tanθ=1/3より

a=tan2θ=2tanθ/(1ーtan^2θ)=2・(1/3)/(1ー(1/3)^2))=(2/3)/(8/9)=3/4

または、点と距離の公式から
y=x/3 上の点(3,1)から、y=axまでの距離が1になればいいので
I a・3ー1 I/√(a^2 +(-1)^2 )
平方して
(3aー1)^2=a^2 +1 ∴ 9a^2ー6a+1=a^2+1 ∴8a^2ー6a=2a(4aー3)=0より
a=0はx軸で不適なので、a=3/4

No.1 回答者： gamma1311 回答日時： 2019/03/29 20:15

53.

1) 重心の座標は、３点の座標の和の1/3です(x, y とも)
2) G(X, Y)=({1+cosθ+cos(θ+pi/2)}/3, {sinθ+sin(θ+pi/2)}/3). ですから、
3X-1=√2*cos(θ+pi/4), 3Y=√2*sin(θ+pi/4). より、
(3X-1)^2+(3Y)^2=2 ... 整理して、軌跡の限界を考慮してください。
54. 左辺第一、第三項をまとめ、sin(3θ)*(2*sinθ+1)>0 を解きます。・・・「２数の積が正」 ⇔ 「２数は同符号」。
55. tanα=1/3 とすると a=tan(2α) です。
56. が最大のヒントです。f(θ)はｔの２次関数。

この回答へのお礼

もう少し詳しく教えていただきたいのです。教えていただけると幸いです。

お礼日時：2019/04/01 08:43