合成インピーダンス

図のように無限につながれた回路において、左から見た合成インピーダンスZの求め方を教えてください

No.2 回答者： yhr2 回答日時： 2016/07/08 12:07

No.1さんの回答で解決していると思うのですが、納得されていないのであれば、もうひと押ししましょう。

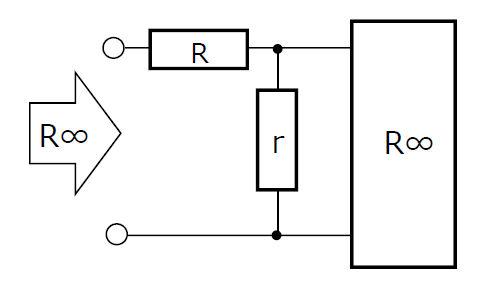
インピーダンスだと複雑そうに見えるので、下図のような抵抗回路で計算してみましょう。「無限につながれている」ので、左から見た抵抗も、右以降につながる抵抗も、同じ「R∞」と書けるはずです。

ということで、
　R∞ = R + rR∞/( r + R∞ )
これを整理すると、
　R∞( r + R∞ ) = R( r + R∞ ) + rR∞
　R∞^2 + rR∞ = rR + RR∞ + rR∞
　R∞^2 - RR∞ - rR = 0

この二次方程式を解くと、解の公式より
　R∞ = [ R ± √(R^2 + 4rR) ]/2
R∞>0 なので
　R∞ = [ R + √(R^2 + 4rR) ]/2
　　　= R/2 + √[ (R/2)^2 + rR ]　　　　（１）
が求める解です。

ご質問の回路の場合には、
　R → R + jωL
　r → 1/jωC = -j/ωC
に置き替えればよいので、

　Z∞ = (R + jωL)/2 + √[ (R + jωL)^2 /4 - j(R + jωL)/ωC ]
　　　= R/2 + jωL/2 + √[ (R^2 + j2ωLR - ω^2 L^2)/4 - jR/ωC + L/C ]
　　　= R/2 + jωL/2 + √[ (R^2/4 - ω^2 L^2/4 + L/C ) + j(ωLR/2 - R/ωC) ]

これ以上は簡単にならないかな？　計算違いがあるかも。
そもそも、（１）の式がこれだけ複雑ですから、お示しの回路ではかなり複雑にならざるを得ません。

No.1 回答者： rnakamra 回答日時： 2016/07/07 11:42

B-B'より右側の回路のインピーダンスをZ'とします。

(B-B'間のコンデンサは無視します)
A-A'間のインピーダンスZはZ'を使い表すと

Z=jLω+R+{1/(jCω+1/Z')}

で、この回路が無限に続くとするとZ'=Zとなります(A-A'間の回路とB-B'間の回路は実質同じ)から、上の式のZ'=Zを代入して得られた方程式を解けばZの式が得られます。