「立方体の６つの面を6色で塗り分ける方法は何通りありますか？」という問題で、答えを見たら、5×(4-

「立方体の６つの面を6色で塗り分ける方法は何通りありますか？」という問題で、答えを見たら、5×(4-1)！で30通りでした。
なぜこのような式になるのでしょう？

質問者からの補足コメント

• 私は最初、6×5×4×3×2×1=720通りだと思っていました。

    補足日時：2018/09/20 16:10

No.5 ベストアンサー 回答者： masterkoto 回答日時： 2018/09/20 17:25

公式と言うより、考え方を押さえてください

４この円順列の場合は東西南北に４つ席がありそこにABCDが座るとします。
北東南西の順に　座り方のパターンは
ABCD
BCDA
CDAB
DABC
などがありますが
これらは右回りに回転するとみんなABCDです。
したがって上記4パターンは同一のものとみなし、右回りにABCDで1通りと数えます。
この他に
ACBD
DACB
BDAC
CBDA
などもやはり回転すれば同じなので同一のものとみなします。
ですから、北東南西に4人を座らせる方法は4!通りとした場合、この中には4通りづつ重複があるのです
これを解消する目的で４！を4で割り
今回求めるべき円順列は
4!/4=(4-1)!・・・公式　
となるのです。

または、初めにAを北に固定して残り3か所にBCDを座らせると考えて
円順列は(4-1)!と考えても良いです。

ここまでが円順列について
ここからは立方体塗り分けについて
6面のうち1面は必ずAと言う色に塗られます。
なので、Aに塗られた面を底面とみなしてしまいます。
すると、上面の決め方はBCDEFと言う色のいずれかで塗られることになるので5通り
仮にBで上面を塗った場合、側面はABの色の面で挟み込まれることになり、これはいくら立体を回転してもABで残り4面を挟み込むことに変わりがありません。
このことから残り4面をはさみこむ色は
AB
AC
AD
AE
AF
の5パターンあることは立体を回転させることには影響を受けません。
だから、A色を底面とみなした場合上面の色の決め方は回転に影響されず5通りとなるのです。

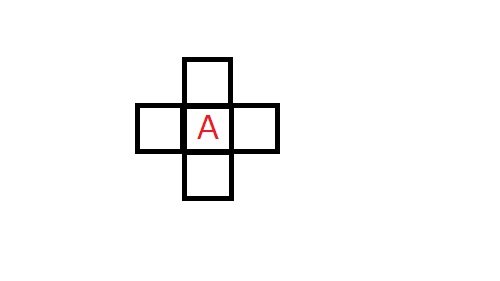
底面と上面が決まったら、立体を切り開いて展開図の状態にします。
画像は上面を省略した展開図です。
これをみると側面の塗り方は前述の円順列そのものですよね！
したがって側面の塗り方は(4-1)!となります。
ABで側面を挟む場合側面の塗り方が(4-1)!
AC、AD,AD,AE,AFで側面を挟む場合もやはり側面の塗り方が(4-1)!ずつ
ゆえに5x(4-1)!通りが塗り分け方の総数となります。

（なお、この5x(4-1)!通りの中には例えば、BCで側面を挟み込むパターンなども既に含まれていますので、5x(4-1)!通り以外に別の塗り分け方は存在しません！）

この回答へのお礼

丁寧に解説してくださってありがとうございます！

お礼日時：2018/09/22 18:09

No.4 回答者： nak_7000 回答日時： 2018/09/20 17:06

組み合わせ勉強し直そうよ

この回答へのお礼

勉強し直します！

お礼日時：2018/09/20 17:07

No.3 回答者： masterkoto 回答日時： 2018/09/20 16:33

底面をA色に決めた時

上面の決め方が5通り
更に、残り4色で塗るから、側面の塗り方は(4-1)!＜＜＜回転すると同じものが現れるから、円順列
あわせて、5×(4-1)！

この回答へのお礼

とにかく円順列の公式を覚えれば解けますね。
ありがとうございます！

お礼日時：2018/09/20 16:36

No.2 回答者： mits0709 回答日時： 2018/09/20 16:30

この問題文だと、あくまで「６面を６色で」塗り分けなくてはいけません。

６×５×４×３×２×１だと、６色全てを使い切れずに５～１色だけになるパターンまで含まれて
しまうのです。

この回答へのお礼

たしかにそうですね！
円順列の考え方でしょうか？
ありがとうございます！

お礼日時：2018/09/20 16:33

No.1 回答者： angkor_h 回答日時： 2018/09/20 16:19

解釈の相違かと思います。

例えば、それを机の上に置いた時、
側面4面の塗順数は、回転させることで1/4に減ってしまいます。
いじわるの一種でしょう。

この回答へのお礼

なるほど！回転しても同じものとする、という事でしょうか。
ありがとうございます！

お礼日時：2018/09/20 16:22