x^2+y^2≦4x , x≦(√3)y を x＝rcosθ+2 , y＝rsinθ として曲座標変

x^2+y^2≦4x , x≦(√3)y　を
x＝rcosθ+2 , y＝rsinθ　として曲座標変換した時のrθ平面での領域を教えてください。

解析学 大学 数学 重積分

No.2 回答者： ゼロプライム 回答日時： 2020/01/24 19:50

x²+y²≦4x……①

x≦(√3)y……②

x＝rcosθ+2……③
y＝rsinθ……④

③、④を①に代入します。
(rcosθ+2)²+(rsinθ)²≦4(rcosθ+2)
r²cos²θ+4rcosθ+4+r²sin²θ≦4rcosθ+8
r²(
r²(cos²θ+sin²θ)≦4
r²≦4
r≦2
これは、極Oを中心とする半径２の円の内部です。(境界線を含みます)……⑤

③、④を②に代入します。
rcosθ+2≦(√3)rsinθ
－rcosθ+(√3)rsinθ≧2
2r{cosθ(-1/2)+sinθ(√3/2)}≧2
2rcos(θ－2π/3)≧2
rcos(θ－2π/3)≧1
極座標が、(1 , 2π/3) の点をAとすると、
rcos(θ－2π/3)=1 は、点Aを通り、OAに垂直な直線です。
よって、不等式 rcos(θ－2π/3)≧1 の表す領域は、直線 rcos(θ－2π/3)=1 の上側部分となります。
(境界線を含みます)……⑥

したがって、求める領域は、⑤と⑥を満たす部分です。
直線の部分が分かりづらいかもしれませんが、図をかいて確かめてください。

No.1 回答者： endlessriver 回答日時： 2020/01/24 17:54

(x-2)²+y²≦4 , y≧x/√3 , (r,θ)に変換すると

r²≦4 → r≦2・・・・①
r≧2/(√3 sinθ-cosθ)・・・②
①②で囲まれた範囲になる。rはθ

1.
①②が一致、r=2となる交点の範囲内なので
2=2/(√3 sinθ-cosθ) → √3 sinθ-cosθ=1 → 2sin(θ-tan⁻¹(1/√3))=1
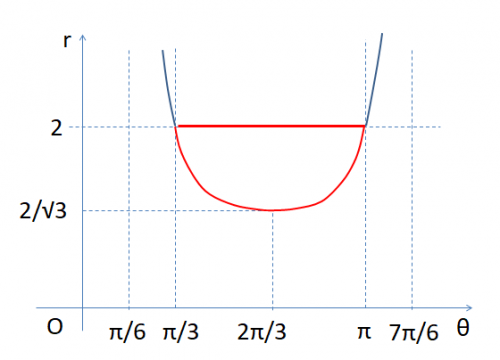
→ sin(θ-π/6)=1/2 → θ-π/6=π/6 or 5π/6 → θ=π/3 or π
となり、θはこの範囲になる。

2.
②はθの関数として凹形状で最小値は
r=2/(√3 sinθ-cosθ)をθで積分して、r'=-{2/(√3 sinθ-cosθ)²}(√3 cosθ+sinθ)=0
→ tanθ=-√3 → θ=2π/3

以上の結果を描くと図のように、赤線の枠内になる。