第一象限内にあって二つの曲線y=x^2 -1 , x^2+y^2+2√3y-1=0と二つの直線y=

第一象限内にあって二つの曲線y=x^2 -1 , x^2+y^2+2√3y-1=0と二つの直線
y=3,x=0
とで囲まれる図形をDとする。

(1)Dの面積を求めよ。

(2)Dをy軸に関して一回転して
得られる回転体の体積を求めよ。

この問題がまったくわかりません。
わかりやすく教えてください

No.3 回答者： guunagoona2015 回答日時： 2015/12/18 21:17

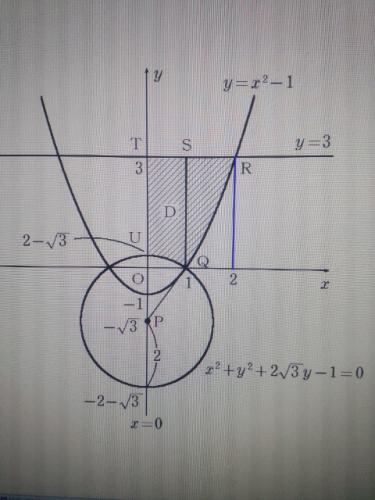
x^2+y^2+2√3y-1=0　より

x^2+(y+√3)^2=4
中心 (0，－√3)、半径 2

（１）　図のように、点Ｐから点Ｕをとると、
(Ｄの面積)＝(台形ＰＱＲＴの面積)－(おうぎ形ＰＱＵの面積)＋(図形ＱＲＳの面積)
ここで、
(台形ＰＱＲＴの面積)＝1/2×{3+(3+√3)}×1＝3+(√3/2)

△ＯＰＱは、ＯＰ：ＰＱ：ＱＯ＝√3：２：１　だから
∠ＯＰＱ＝30°
よって、
(おうぎ形ＰＱＵの面積)＝π×2^2×(30/360)＝π/3

(図形ＱＲＳの面積)＝∫[1→2]{3－(x^2－1)}dx＝∫[1→2](4－x^2)dx
＝[4ｘ－(1/3)ｘ^3][1→2]＝{8－(8/3)}－{4－(1/3)}＝5/3

したがって、
(Ｄの面積)＝3+(√3/2)＋π/3＋5/3＝(28+3√3+2π)/6


（２）(求める体積)＝(図形ＯＱＲＴをｙ軸まわりに１回転した体積)－(図形ＯＱＵをｙ軸まわりに１回転した体積)
ここで、
(図形ＯＱＲＴをｙ軸まわりに１回転した体積)
＝∫[0→3]πx^2dy
＝π∫[0→3](y+1)dy
＝π{(1/2)y^2+y}[0→3]
＝π{(9/2)+3}
＝(15/2)π

(図形ＯＱＵをｙ軸まわりに１回転した体積)
＝∫[0→2－√3]πx^2dy
＝π∫[0→2－√3](－y^2－2√3y+1)dy
＝π{－(1/3)y^3－√3y^2+y}[0→2－√3]
＝－π{(1/3)(2－√3)^3+√3(2－√3)^2－(2－√3)}
＝－π{(1/3)(8－12√3＋18－3√3)+√3(4－4√3+3)－2+√3}
＝－π{(26/3)－5√3+7√3－12－2+√3}
＝－π{－(16/3)+3√3}
＝{(16/3)－3√3}π

したがって、求める体積は、
(15/2)π－{(16/3)－3√3}π＝{(13/6)+3√3}π

になるのではないでしょうか。

No.2 回答者： sakuranoyoru 回答日時： 2015/12/17 16:12

難しい、、、分かりません(；´Д｀)

No.1 回答者： tekcycle 回答日時： 2015/12/15 03:49

解いてませんが、

この問題が解らないのか、この問題以前の所からさっぱり解らないのか、明確にして下さい。
この問題が解らないなら、どこまでのことをやってみて、どこから解らないのか、明確にして下さい。
なお、x^2+y^2+2√3y-1=0が円の方程式だということに気付いているでしょうか？

教科書の、積分とは、という辺りで、幅がΔｘの短冊というか台形というか、それを積み重ねていく、という話があったと思います。
基本はその通りで、短冊を積み重ねていくのです。
幅がΔｘの短冊を考えるのであれば、短冊の高さの式がどうなるのかを出せばいい。
短冊の高さかけるΔx、で短冊の面積が表せます。
それを、インテグラルしてやる、積み重ねてやると(短冊の高さの式をｆ(ｘ)とすると)、
∫ｆ(ｘ)ｄｘ
となるのです。ここからはどこかで見たことがあるでしょう。
後はこれを計算してやればいい。
短冊の高さはどうなっているのか！式で表せ！ってことでしょう。

回転体は、短冊の代わりに、千切りの大根みたいな物を想像すると良いでしょう。
幅がΔｙの短冊、ではなく薄切りたくあん。
薄切りたくあんの面積の式は何か。
回転体ですから円ですよね。円の面積は、半径の二乗かけるπ。
つまり、半径の式は何か、って事です。
ただし、おそらく中空になるんでしょう。ドーナツ状。
外側の円から内側の円の面積を引いてやればいい。
そして同様に、その面積×Δｙが薄切りたくあんの体積で、そいつをインテグラルしてやればいい。
∫ｇ(ｙ)ｄｙ
たくあんの面積の式はどうなっているのか！ってことでしょう。

んじゃぁ、この、どこからできないのか、ということです。
できないところから勉強しないといけません。