この問題なのですが、3番です。 どういうことを言ってるのかわかりません…教えてください。

この問題なのですが、3番です。
どういうことを言ってるのかわかりません…教えてください。

質問者からの補足コメント

• お願いします！

  
    補足日時：2018/09/23 23:20

• 問題です

  
    補足日時：2018/09/23 23:21

No.2 ベストアンサー 回答者： masterkoto 回答日時： 2018/09/24 15:39

x²-2x≦0・・・① より

x(x-2)≦0
⇔0≦x≦２・・・②
ｘが②の範囲内の数値ならばどんな数であっても
ｆ＝x²-2ax+3a>0が成り立つようにaを定めろという事です。
つまり、
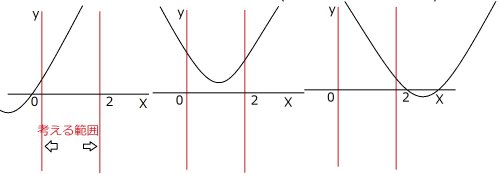
ｆ＝(x-a)²-a²+3a(頂点(a,-a²+3a)）のグラフが、画像のようにx=0からx=2の帯の中ではx軸よりも上にあるようにaを定めろと言うこと
そこで場合分けして考える
1．頂点がx=0からx=2の帯より左の場合
頂点のx座標を見て　a<0で　図左よりx=0でグラフが0より大きければ帯内ではf>0となるから　f(0)＞０でなければならない
f(0)=3a>0⇔a>0だから
a<0かつa>0となるようなaは存在しない・・・１．の場合題意を満たすaは存在しない
２．頂点が帯の中にある場合
頂点のｘ座標から0≦a≦2で　図中央より　頂点がx軸より上にあれば良いから
-a²+3a>0⇔a(a-3)<0⇔0<a<3
共通範囲は0<a≦2
3.頂点が帯より右の場合
頂点のx座標を見て　2<a
図右よりf(2)＞０でなければならないから
f(2)=4-a>0⇔4>a
共通範囲は2<a<4
1.2.3の範囲を合わせて0<a<4
このような題意と解法になりますよ！＾＾

No.1 回答者： Worst_Answer 回答日時： 2018/09/23 21:15

何が書いてあるのか読めません・・・教えてください。