電気鏡像の問題です。

QMとQLの２つの電荷が作る電気鏡像は原点を中心とする半径rの球形導体が無限遠点のゼロ電位に接地されて固定されている場合と同じである。
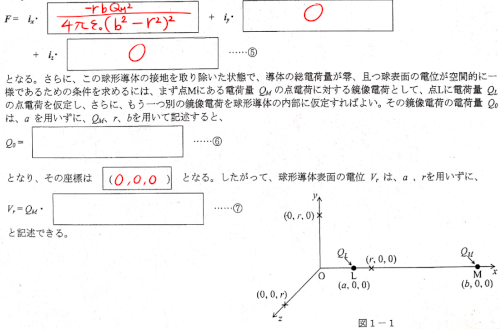
その時、球形導体および点電荷の質量が無視できるものとすると、点Mの点電荷に働く力Fは、x軸、ｙ軸、ｚ軸のそれぞれの正方向の単位ベクトルix,iy,iz,およびQM, r, b, ε0を用いて（aを用いずに）記述すると
以下問題に続きます。
赤文字は赤文字は自分が埋めたものです。
接地を取り除くとんどうなるのかが全くわかりません。
球の表面の電位を保ったまま内部に電荷を置くとしたら中心しかないと考えて座標だけ埋めましたが、上下の空欄の解き方、考え方がわからないので教えていただきたいです。
何卒よろしくお願い致します。

No.1 ベストアンサー 回答者： rnakamra 回答日時： 2021/04/15 12:38

>球の表面の電位を保ったまま内部に電荷を置くとしたら中心しかないと考えて

これは正しい。

導体の総電荷量は球体内部にある鏡像電荷の総量となります。
総電荷量はQL+Qoですのでこれが0であるなら
QL+Qo=0→Qo=-QL
となります。

球形導体の表面電位はQM,QL,Qoのつくる電位の和になりますが、QMとQLが作る電位の和は無限遠点と同じですから無視してよくQoの作る電位だけを計算すればよい。

この回答へのお礼

ありがとうございました。
理解することができました

お礼日時：2021/04/17 00:19

No.3 回答者： syotao 回答日時： 2021/04/16 19:26

Nｏ2の説明誤解ありました。

ごめんなさい。

No.2 回答者： syotao 回答日時： 2021/04/16 18:31

球体のすぐ外側の電場は球体が等電位だからこの球面に対して垂直

したがってこの球面と内部の電荷に対してガウスの定理をはめれば
、表面積分は0
ところが
原点にあるQoとＱLとＱM　がなす電場が電荷0の球体の外側の電場
だからこの表面積分はQo＋ＱLを真空誘電率でわったものになるから
Qo＋ＱL＝0　になるわけやね。

この回答へのお礼

ありがとうございました

お礼日時：2021/04/17 00:20