線形代数 二次曲線の概形を描く問題 x^2+10√3xy+11y^2=8 手順を丁寧に教えていただき

線形代数
二次曲線の概形を描く問題

x^2+10√3xy+11y^2=8

手順を丁寧に教えていただきたいです

No.2 ベストアンサー 回答者： majimelon37 回答日時： 2018/07/27 23:00

二次曲線の概形を描く問題

x^2+10√3xy+11y^2=8
No.1の投稿はx^2+10√(3xy)+11y^2=8と誤解しているので、二次曲線にはなりません。
二次曲線だから、√の記号は3だけにかかり、曲線の方程式は①となる。
行列式等はこの投稿システムではうまく表示されないので、図の①～
グラフは楕円または双曲線を表す。実は双曲線になることは、以下の計算により証明される。
x^2+10(√3)xy+11y^2=8＿＿①
両辺を8で割ると②となり、③の形となる。
(1/8)x^2+2(5√3/8)xy+(11/8)y^2=1＿＿②
a x^2+2bxy+cy^2=1＿＿③
a=1/８，b=5√3/8，c=11/8＿＿④
二次曲線の問題には、普通、行列計算を使うので、まず、行列を使って解く方法を示すが、もし、質問者が、行列計算を知らない場合は、後に記す別解を見て下さい。
また、行列表示は、うまく表示されないので、式①~⑫は図を参照して下さい。
(x,y)は横ベクトルで、tをベクトルの転置記号として、t(x,y)を(x,y)の縦ベクトルとする。
１、行列表示
行列Aを⑤とすると、式③は行列の形式⑥となる。
A=( a b　=( 1/８ 5√3/8　＿＿⑤
　　 b　c )　　5√3/8　11/8 )
(x,y)A t(x,y) = a x^2+2bxy+cy^2=1＿＿⑥
２、固有方程式と固有値
行列Aから次の行列式det(A－λI)を作る。Iは単位行列である。これを特性多項式という。
| a－λ　ｂ　 | =( a－λ)( c－λ)－ｂ^２＿＿⑦
| ｂ　　 c－λ |
=( a－λ)( c－λ)－ｂ^２=０＿＿⑧
⑧を特性方程式（または固有方程式)という。
固有方程式の解を固有値といい、式⑩に示す2と－1/2となる。
(a－λ)(c－λ)－ｂ^２=λ^２－( a+ c)λ+ac－ｂ^２
=λ^２－(3/2)λ+11/64－75/64=λ^２－(3/2)λ－1=0＿＿⑨
λ=3/4±√((3/2)２+4)/2=3/4±√((3/2)２+4)/2
=3/4±√(25/4)/2=3/4±5/4=3/4±5/4=2，－1/2＿＿⑩
この二つの固有値をλ1，λ2とすると、楕円、双曲線の方程式の標準形は⑪となる。
u^２/λ１+v^２/λ２=１＿＿⑪
λ１>0，λ２>0のときは⑪は楕円の方程式になるが、この問題では、
⑩により固有値はλ1=2,λ2=－1/2だから、⑪は双曲線の方程式⑫となる。
u^２/a^２－v^２/ｂ^２=１，a=√λ1=√2，b=√(－λ2)=1/√2＿＿⑫
３、固有ベクトル
投稿を書くのにかかる時間が取れないので、とりあえず、ここまでで投稿する。以下は改めて投稿する。

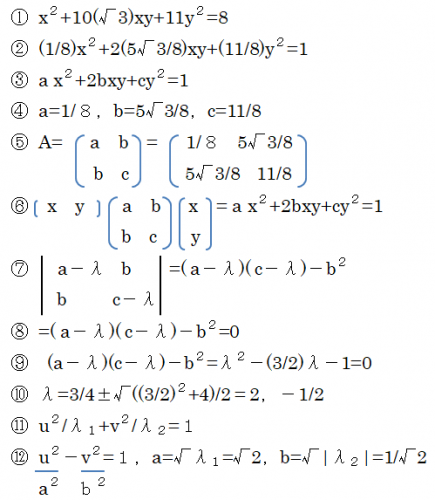
No.3 回答者： afilter 回答日時： 2018/07/28 17:31

x^2+10√3xy+11y^2=8

点(x,y)を、座標軸をθ回転させたXY座標上で見た座標を(X,Y)とすると、
x=Xcosθ-Ysinθ
y=Xsinθ+Ycosθ
なる関係が成立する。

x^2+10√3xy+11y^2= x^2+y^2+10√3xy+10y^2
=X^2+Y^2+10√3((X^2-Y^2)sinθcosθ+XY((cosθ)^2-(sinθ)^2))
+10(X^2(sinθ)^2 +Y^2(cosθ)^2+2XYsinθcosθ)=8

X^2+Y^2+5√3((X^2-Y^2)sin2θ+2XYcos2θ)
+5(X^2 +Y^2+(Y^2-X^2)cos2θ+XYsin2θ)=8

6X^2+6Y^2+5√3((X^2-Y^2)sin2θ+XYcos2θ)
+5(Y^2-X^2)cos2θ+5XYsin2θ=8

6X^2+6Y^2+5√3((X^2-Y^2)sin2θ+5(Y^2-X^2)cos2θ
+5XY(sin2θ+√3cos2θ)=8

XY の項が消えるθを求めると、 tan(2θ)=-√3より θ=-30°となる。
θ=-30°を上式に代入して次式を得る。

-X^2/2+2Y^2=1

座標軸をθ=-30°（時計方向に30°）回転させたXY座標上で、標準形となった双曲線を描けばよい。

No.1 回答者： yhr2 回答日時： 2018/07/26 12:55

このままでも、

x= -3, -2, -1, 0, 1, 2, 3
で各々対応する y を求め、グラフ用紙にプロットすれば概形が書けますよ。
もっと細かくしたいなら、どんどん細分化していけばよいし。

x=0 なら
　11y^2 = 8
より
　y = ± 2√(2/11)

y=0 なら
　x^2 = 8
より
　x = ± 2√2

と求まります。

「理解不能！」なんていうことはあり得ないと思いますが。

もちろん、与えられた式から
・√(3xy) という項があるので
　3xy ≧ 0
つまり
　xy ≧ 0
なので、「第１象限」「第３象限」（x, y軸も含む）に限定される。

・x^2 + 11y^2 = 8 - 10√(3xy)
なので
　8 - 10√(3xy) ≧ 0
よって
　√(3xy) ≦ 4/5
従って
　0 ≦ 3xy ≦ 16/25
→　0 ≦ xy ≦ 16/75

・x^2 + 11y^2 = 8 - 10√(3xy) ≦ 8
なので、
　x^2 + 11y^2 ≦ 8
つまりは
　-2√2 ≦ x ≦ 2√2
　-2√(2/11) ≦ y ≦ 2√(2/11)

などということも分かりますが、これらは「グラフの範囲」であって「グラフそのもの」ではありません。

グラフの形を調べるには、微分して「極値」や「変曲点」を求める方法もあります。

概形なのですから、いろいろな手順で、「だいたいこんな形」ということを追い込んでいけばいいんですよ。
いくつかの代表点の座標は、最初のように数値計算で求めればよいし。

「理解不能」なんて言ってないで、とにかく「ジタバタ」してみること！