現在、大学1年で基礎力学を履修しているものです。よろしくお願いします。
問題は、「質量mの質点が速度vで位置rを通過するとき、ある点(位置Rとする)のまわちの角運動量Lは{L=m(r-R)×v}である。したがって位置rが時刻tの関数として与えられるとき、角運動量は、{L=m(r-R)×v}の式を使って計算することができる。質量mの質点が図のような運動をしているとき、指定された点のまわりの角運動量を求めよ。((a),(b)の各場合において、ベクトルの外積を計算することによって角運動量を(Lx、Ly,Lz)の形で成分表示せよ。そのあと角運動量の大きさと向きを答えよ。ただし図において奥から手前の向きを+zの向きとする)」
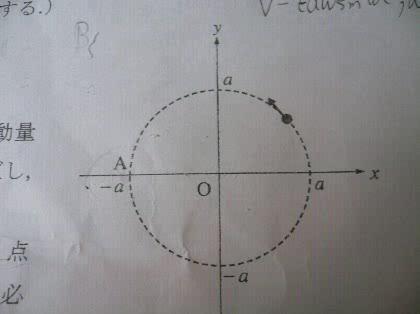
(a)xy平面で原点を中心とする円運動{r=(acosωt,asinωt,0)}をしている質点において、原点のまわりの角運動量(m、a、ω、tのうち必要な文字を使ってあらわせ)ただしa、ωはともに正の定数。
(b) (a)と同じ運動をしている質点について、点A(-a,0,0)のまわりの角運動量(m、a、ω、tのうち必要な文字を使ってあらわせ)
という問題です。(a)の外積は{r=(acosωt,asinωt,0)}を微分して、vを求めればわかるんですが、残りの角運動量の大きさと向きというのがわかりません
お探しのQ&Aが見つからない時は、教えて!gooで質問しましょう!
似たような質問が見つかりました
- 物理学 角運動量の定義式 4 2022/12/18 05:36
- 物理学 高1力学の運動量の問題です。問題を一通り解いたのですが、行き詰まってしまったのでご回答頂ければ嬉しい 3 2022/06/29 11:20
- 物理学 角運動量の式変形が分かりません。 4 2022/08/03 21:04
- 物理学 面積速度一定の法則を(1/2)r v sinθを使って証明する方法 2 2023/06/25 12:43
- 物理学 長さaの軽い棒の各端に質量mの物体A,Bを取り付け、なめらかな床の上におき、これを棒の中点Oを中心と 2 2022/10/09 19:16
- 物理学 力学的エネルギー保存則について 4 2023/06/06 14:02
- 物理学 質量 M,半径αの円板が1つの直径を固定軸として回転できるようになっている。質量mの物体が速さvで円 2 2022/10/21 20:16
- 物理学 図のように、内半径aの中空の円筒が、その中心軸が水平になるように固定されており、その中で、 質量 M 7 2023/02/15 09:23
- 物理学 物理基礎で、力学的エネルギーと動摩擦力のことを習ったのですが、 あらい斜面の下から物体を滑り上がらせ 2 2022/09/11 10:12
- 高校 円運動の質問 4 2022/05/02 04:53
おすすめ情報
デイリーランキングこのカテゴリの人気デイリーQ&Aランキング
マンスリーランキングこのカテゴリの人気マンスリーQ&Aランキング
-
基本ベクトルと単位ベクトルの...
-
ベクトル関数の概略を図示せよ...
-
大学物理の問題について
-
空間以外のベクトル
-
重心と質量中心の違いについて
-
波数の意味と波数ベクトル
-
三相交流の仕組みが調べても理...
-
ブリュアンゾーンの物理的な意味
-
ヤコビアンが
-
物理の力や速度は何故ベクトル...
-
ミラー指数:面間隔dを求める式...
-
速度ベクトルの単位の書き方
-
電荷と電束、磁荷と磁束について
-
角速度のベクトルの方向は何故...
-
力のモーメントのつりあいで 鉛...
-
なぜ、エネルギーはスカラーで...
-
波数ベクトル
-
ベクトル量とスカラー量の判定方法
-
物理の、速度の問題です。
-
ベクトルの太文字書きについて...
おすすめ情報
