楕円の共通部分の面積

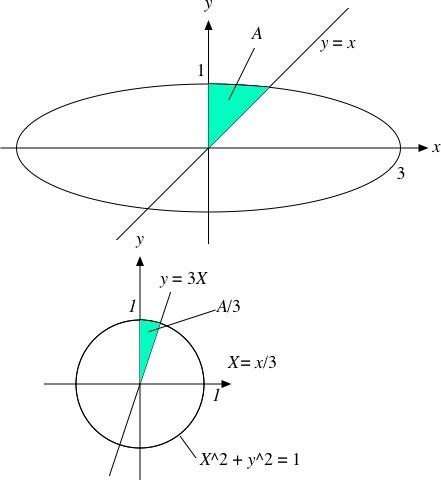
短径1、長径3、中心(0.0)の楕円と、原点中心にこれを90°回転させた楕円の共通部分の面積を求めたいです。
短径1、長径3、中心(0.0)の楕円を(1):x^2+(y^2)/3=1
90°回転させた図形を(2):(x^2)/3+y^2=1
とした時、(1)と(2)の第一象限での交点が(√3)/2であることを利用して、
4{integrate (1-(x^2)/3)^(1/2) dx from 0 to (√3)/2 }
+ 4{integrate (3-3(x^2))^(1/2) dx from (3^(1/2))/2 to 1}
で求められる、という考えでいいでしょうか。

(この計算結果は1/3(2√3π)となりました。)

No.4 回答者： stomachman 回答日時： 2013/07/20 02:27

積分を使わないで計算できるでしょ。

図上の緑の部分の8倍が求める面積ですよね。図下のように、ヨコ軸を1/3に縮小してやれば、楕円は円になり、緑の部分の面積は1/3になります。これなら簡単に計算できる。

この回答へのお礼

ありがとうございます。

お礼日時：2013/08/01 20:48

No.3 ベストアンサー 回答者： info22_ 回答日時： 2013/07/19 14:00

No.2です。

ANo.2の補足の訂正
>長軸2√3の間違いでした。短軸の長さはあっています。

をした後の楕円の式は
質問の中の
(1):x^2+(y^2)/3=1
(2):(x^2)/3+y^2=1
の式になりますので

>(1)と(2)の第一象限での交点が(√3)/2であることを利用して、
面積Sは
>4{integrate (1-(x^2)/3)^(1/2) dx from 0 to (√3)/2 }
+ 4{integrate (3-3(x^2))^(1/2) dx from (3^(1/2))/2 to 1}
で求められる、という考えでいいでしょうか。

という考えで良いでしょう。

計算結果も
>この計算結果は1/3(2√3π)となりました。
で合っています。

なお、共通領域の対称性から面積Sは
8integrate (1-(x^2)/3)^(1/2)-x dx from 0 to (√3)/2
でも、求められます。

この回答へのお礼

ありがとうございます。

お礼日時：2013/08/01 20:47

No.2 回答者： info22_ 回答日時： 2013/07/19 13:12

短径1、長径3、中心(0.0)の楕円の式は

(1):x^2+(y^2)/3=1
ではありません。

短径1、長径3、中心(0.0)の楕円を原点中心にこれを90°回転させた楕円の式は
(2):(x^2)/3+y^2=1
でありません。

また
楕円の式を
x^2/a^2+y^2/b^2=1
0<a<bとおくと、短軸の長さ2aを短径、長軸の長さ2bを長軸と言います。
（参考URLをみて楕円の短径と短軸、長径と長径の定義と楕円の標準形のa,bとの関係を確認してください。）

問題文通りの楕円の式(1)と(2)は
(1) x^2/(1/2)^2 +y^2/(3/2)^2=1　...(※1)
(2) x^2/(3/2)^2 +y^2/(1/2)^2=1　...(※2)
となります。

楕円の式が間違って入れば、問題文を訂正して補足にお書きください。
問題文が正しければ、(※1),(※2)の式を用いて、計算し直して、補足に書き直して頂ければチェックいたします。

参考URL：http://ja.wikipedia.org/wiki/%E6%A5%95%E5%86%86

この回答への補足

長軸2√3の間違いでした。短軸の長さはあっています。すみません。

補足日時：2013/07/19 13:16

No.1 回答者： hashioogi 回答日時： 2013/07/19 13:10

(1):x^2+(y^2)/3=1

は本当は
(1):x^2+(y^2)/9=1
が正しくないですか？