幾何の問題

Question

辺AB=BC=CDの時，∠BCDの大きさを求めよ．
(図を添付しております)

という問題です。

補助線AC、BDを引いたりしましたが、全く解けませんでした。
どなたわかる方がいらっしゃいましら、ご教授お願いします。

naniwacchi · Accepted Answer

算数オリンピックで出てきそうな問題ですね。

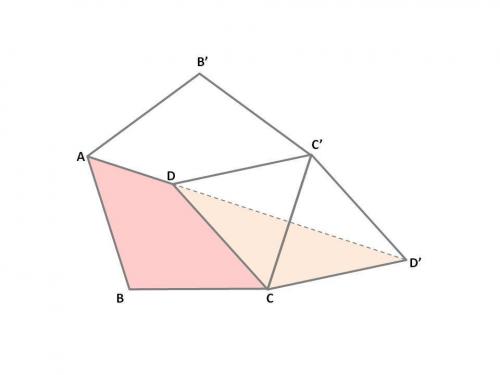
補助線を引くのではなく、辺ADで折り返した図形を考えてみてください。
（2つの四角形が辺ADでつながっている形）

折り返した図形を四角形ADC’B’とし、CC’を結びます。
すると、正〇角形が 2つ現れます。（大きいものと小さいもの）
この図が描ければ、難しい計算にはなりません。

108＝ 54×2や等しい長さの辺の位置に注意してみてください。

watecolor1969 · Answer

正五角形の１つの内角が108°という事実
を知っていれば、ANo.1(ANo.4)さんのやり方
が最も理にかなっている気がしますが、
あえて、別の方法で記しておきます。

ラフに書いたので適当に修正してください。

まず、辺AD、BCをそれぞれ右に伸ばしていき
交わった点をEとします。

次に点Cを中心に半径CB（=CD）の円を描きます。

その上で点Cから線分AEと直角になるように線を引き、
線分AEとの交点をG、円との交点をFとします。

また、円と線分AEとの交点をHとし、
線分CH、FHを引きます。
この時、CD = CHより△CDHは二等辺三角形であり
また△CDG≡△CHG　…(1)

さらに、線分ACと線分AFを追加します。

ここで、∠BEA = 180°- (108°+54°) = 18°(=∠CEG)
また、△BACが二等辺三角形であることより
∠BAC = (180°- 108°) / 2 = 36°
∴∠DAC = 54°- 36°= 18°(=∠CAG)
これから、△CAEは二等辺三角形であり
CA = CE で△CAG≡△CEG。

今、∠FCE = 180°- ∠CEG - ∠EGC = 180°- 90°- 18°= 72°
よって、∠BCF = 180°- ∠FCE = 180°- 72°= 108°
なおかつ　BA = CF より　AF // CE
平行線の錯覚が等しいことより
∠CEG = ∠FAG = 18°△CAFは二等辺三角形で
△CAG≡△FAG(≡△CEG)

よって CG = FG から△CDG≡△FDG（≡CHG）
従って CD = FD = CF（円の半径） となり
△CDFは正三角形であり∠DCF(∠DCG) = 60°

従って、X°= ∠BCD = ∠BCF - ∠DCF = 108°- 60°=48°

また　　X°= ∠BCH = ∠BCD + ∠DCG + ∠HCG = 48°+ 60°+ 60°= 168°
　　　　　　　（∵(1)より）

答え：X = 48°または X = 168°

naniwacchi · Answer

#1です。
自分の中での整理も含めて。

#2さんの方法はわたしも解けませんでした。
三角関数を使うにしても、数値計算になってしまうかと。

#3さんの2つの答えは、正三角形を折り返すことで説明ができます。
もとの四角形がだいぶ違う印象になります。

uen_sap · Answer

結構難しい

解は二つ

４８度、１６８度

ORUKA1951 · Answer

「ひらめき」なんか使わずに、普通に計算して解く方法。
1) 三角形BCDは二等辺三角形なので、∠DBC = ∠BDC
　^^^^^^^^^^^^^^^^^^^^^^^^^^^^
2) ∠ABD = 108°- ∠DBC
3) ∠DAB + ∠BDA + ∠ABD = 180°(三角形の内角の和)
以上から、計算できますよ。

幾何の問題

算数オリンピックで出てきそうな問題ですね。

正五角形の１つの内角が108°という事実

#1です。

結構難しい

「ひらめき」なんか使わずに、普通に計算して解く方法。

関連するカテゴリからQ&Aを探す

デイリーランキングこのカテゴリの人気デイリーQ&Aランキング

マンスリーランキングこのカテゴリの人気マンスリーQ&Aランキング