この英文の和訳をお願いします。

To avoid this difficulty, we consider the scale height to be (i+αr_G) rather than i, where α is a numerical factor; α must have a value of the order of 10 to be consistent with Eq. (35). For the requirements that in the limit of i=0, <P(e,i)>_2B has to naturally tend to <P(e,0)>_2B given by Eq. (28), we put the modified collisional rate in the two-body approximation to be

<P(e,i)>_2B=Cπr_p^2{1+6/(r_p(e^2+i^2))}(e^2+i^2)^(1/2)/(2(i+ατ_G)) 　　　　　　　　　　 (36)

with

C=((2/π)^2){E(k)(1-x)+2αE(√(3/4))x}, 　　　　　　　　　　　　　　　(37)

where x is a variable which reduces to zero for i>>αr_G and to unity for i<<αr_G. The above equation reduces to Eq. (29) when i>>αr_G while it tends to the expression of the two-dimensional case (28) for i<<αr_G. Taking α to be 10 and x to be exp(-i/(αr_G)), <P(e,i)> scaled by Eq. (36) is shown in Fig. 17. Indeed, the modified <P(e,i)>_2B approximates <P(e,i)> within a factor of 5 in whole regions of the e-I plane, especially it is exact in the high energy limit (v→∞). However, two peaks remain at e≒1 and i≒3, which are closely related to the peculiar features of the three-body problem and hence cannot be reproduced by Eq. (36).

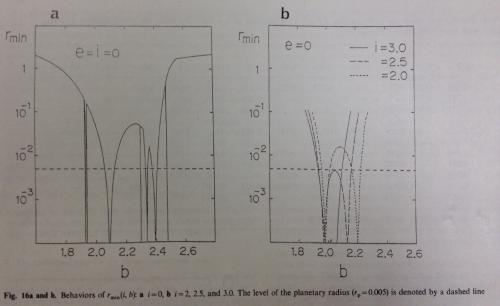
Fig. 16a and b. Behaviors of r_min(i,b): a i=0, b i=2, 2.5, and 3.0. The level of the planetary radius (r_p=0.005) is denoted by a dashed line.

Fig. 17. Contours of <P(e,i)> normalized by the modified <P(e,i)>_2B given by Eq. (36).

Fig. 16a and b.↓
http://www.fastpic.jp/images.php?file=4940423993 …
Fig. 17.↓
http://www.fastpic.jp/images.php?file=5825412982 …

よろしくお願いします。

No.1 ベストアンサー 回答者： ddeana 回答日時： 2013/10/03 12:56

この問題を避ける為に、スケールハイトはiよりもむしろ((i+αr_G)になるものと我々は考える。

その場合αはひとつの数値因子であり、方程式(35）と一致するよう10のオーダーの数値でなくてはならない。i=0という制限の中でのものという必要条件の為、<P(e,i)>_2Bは自然と方程式(28)で与えられた<P(e,o)>_2Bになっていくはずであり、我々は下記になるよう二体近似に修正した衝突速度をあてはめてみる。

<P(e,i)>_2B=Cπr_p^2{1+6/(r_p(e^2+i^2))}(e^2+i^2)^(1/2)/(2(i+ατ_G)) 　(36)　　　　　そして
C=((2/π)^2){E(k)(1-x)+2αE(√(3/4))x}　(37)

ここでのxは、iがαr_Gよりも非常に大きい場合ゼロに近づいていき、iがαr_Gよりも非常に小さい場合集合体へと減っていく変数である。上記数式はiがαr_Gよりも非常に大きい場合方程式(29）へと変っていく一方iがαr_Gよりも非常に小さくなる為の二次元ケース(28)の式でもある。αを10と考え、xを数式(-i/αr_g)と考えながら、方程式(36)で縮尺化された<P(e,i)>は図17で示してある。事実、e-i平面全体の領域において修正された<P(e,i)>_2Bは、5倍以内で<P(e,i)>に近く、特に高エネルギー限界（vが無限大へと向かう）ではまさしく同じである。しかしながらeが1とほぼ等しく、iが3とほぼ等しいところでは二つのピークは残っており、これは3体問題独特の構造と密接に関連しており、よって方程式(36)により再構成することは出来ない。

図16.aおよびb：r_min(i,b)の動き。a iは0, b iは2, 2.5そして3.0である.　惑星の半径のレベル(r_pは0.005)は点線で示してある。

図17：方程式(36）で与えられた修正済み<P(e,i)>_2Bにより正規化された<P(e,i)>の等高線

この回答へのお礼

遅くなりましたが、ご丁寧に和訳してくださり、大変ありがとうございました。

お礼日時：2013/11/07 14:15